
← return to study.practicaldsc.org
The problems in this worksheet are taken from past exams in similar
classes. Work on them on paper, since the exams you
take in this course will also be on paper.
We encourage you to
attempt these problems before Tuesday’s exam review
session, so that we have enough time to walk through the solutions to
all of the problems.
We will enable the solutions here after the
review session, though you can find the written solutions to these
problems in other discussion worksheets.
Nishant decides to look at reviews for the Catamaran Resort Hotel and Spa. TripAdvisor has 96 reviews for the hotel; of those 96, Nishant’s favorite review was:
"close to the beach but far from the beach beach"What is the TF of "beach" in Nishant’s favorite review?
Give your answer as a simplified fraction.
Answer: \frac{3}{10}
The answer is simply the proportion of words in the sentence that are
the word "beach". There are 10 words in the sentence, 3 of
which are "beach".
The TF-IDF of "beach" in Nishant’s favorite review is
\frac{9}{10}, when using a base-2
logarithm to compute the IDF. How many of the reviews on TripAdvisor for
this hotel contain the term "beach"?
3
6
8
12
16
24
32
Answer: 12
The TF-IDF is the product of the TF and IDF terms. So if the TF-IDF
of this document is \frac{9}{10}, and
the TF is \frac{3}{10}, as established
in the last part, the IDF of the term "beach" is 3. The IDF
for a word is the log of the inverse of the proportion of documents in
which the word appears. So, since we know there are 96 total
documents.
3 = log_{2}(\frac{96}{\text{\# documents containing "beach"}})
2^{3} = \frac{96}{\text{\# documents containing "beach"}}
\boxed{12} = {\text{\# documents containing "beach"}}
The DataFrame below contains a corpus of four song titles, labeled from 0 to 3.

What is the TF-IDF of the word "hate" in Song 0’s title?
Use base 2 in your logarithm, and give your answer as a simplified
fraction.
Answer: \frac{1}{6}
There are 12 words in Song 0’s title, and 2 of them are
"hate", so the term frequency of "hate" in
Song 0’s title is \frac{2}{12} =
\frac{1}{6}.
There are 4 documents total, and 2 of them contain
"hate" (Song 0’s title and Song 3’s title), so the inverse
document frequency of "hate" in the corpus is \log_2 \left( \frac{4}{2} \right) = \log_2 (2) =
1.
Then, the TF-IDF of "hate" in Song 0’s title is
\text{TF-IDF} = \frac{1}{6} \cdot 1 = \frac{1}{6}
Which word in Song 0’s title has the highest TF-IDF?
"i"
"hate"
"you"
"love"
"that"
Two or more words are tied for the highest TF-IDF in Song 0’s title
Answer: Option A: "i"
It was not necessary to compute the TF-IDFs of all words in Song 0’s
title to determine the answer. \text{tfidf}(t,
d) is high when t occurs often
in d but rarely overall. That is the
case with "i" — it is the most common word in Song 0’s
title (with 4 appearances), but it does not appear in any other
document. As such, it must be the word with the highest TF-IDF in Song
0’s title.
Let \text{tfidf}(t, d) be the TF-IDF of term t in document d, and let \text{bow}(t, d) be the number of occurrences of term t in document d.
Select all correct answers below.
If \text{tfidf}(t, d) = 0, then \text{bow}(t, d) = 0.
If \text{bow}(t, d) = 0, then \text{tfidf}(t, d) = 0.
Neither of the above statements are necessarily true.
Answer: Option B
Recall that \text{tfidf}(t, d) = \text{tf}(t, d) \cdot \text{idf}(t), and note that \text{tf}(t, d) is just $ (t, d) $. Thus, \text{tfidf}(t, d) is 0 is if either \text{bow}(t, d) = 0 or \text{idf}(t) = 0.
So, if \text{bow}(t, d) = 0, then \text{tf}(t, d) = 0 and \text{tfidf}(t, d) = 0, so the second option is true. However, if \text{tfidf}(t, d) = 0, it could be the case that \text{bow}(t, d) > 0 and \text{idf}(t) = 0 (which happens when term t is in every document), so the first option is not necessarily true.
Below, we’ve encoded the corpus from the previous page using the bag-of-words model.
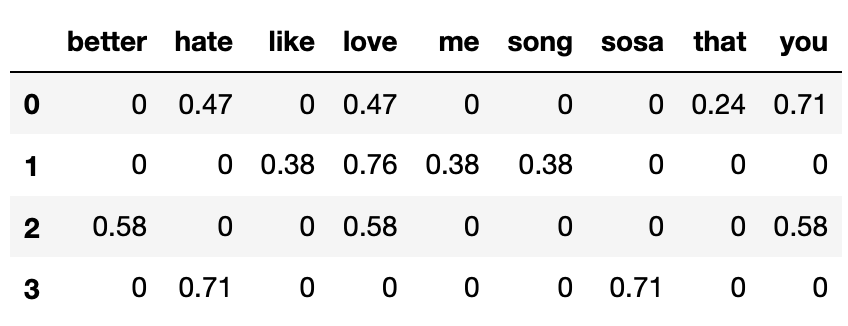
Note that in the above DataFrame, each row has been normalized to have a length of 1 (i.e. |\vec{v}| = 1 for all four row vectors).
Which song’s title has the highest cosine similarity with Song 0’s title?
Song 1
Song 2
Song 3
Answer: Option B: Song 2
Recall, the cosine similarity between two vectors \vec{a}, \vec{b} is computed as
\cos \theta = \frac{\vec{a} \cdot \vec{b}}{| \vec{a} | | \vec{b}|}
We are told that each row vector is already normalized to have a length of 1, so to compute the similarity between two songs’ titles, we can compute dot products directly.
Song 0 and Song 1: 0.47 \cdot 0.76
Song 0 and Song 2: 0.47 \cdot 0.58 + 0.71 \cdot 0.58
Song 0 and Song 3: 0.47 \cdot 0.71
Without using a calculator (which students did not have access to during the exam), it is clear that the dot product between Song 0’s title and Song 2’s title is the highest, hence Song 2’s title is the most similar to Song 0’s.
The DataFrame dogs, contains one row for every
registered pet dog in Zurich, Switzerland in 2017.
The first few rows of dogs are shown below, but
dogs has many more rows than are shown.
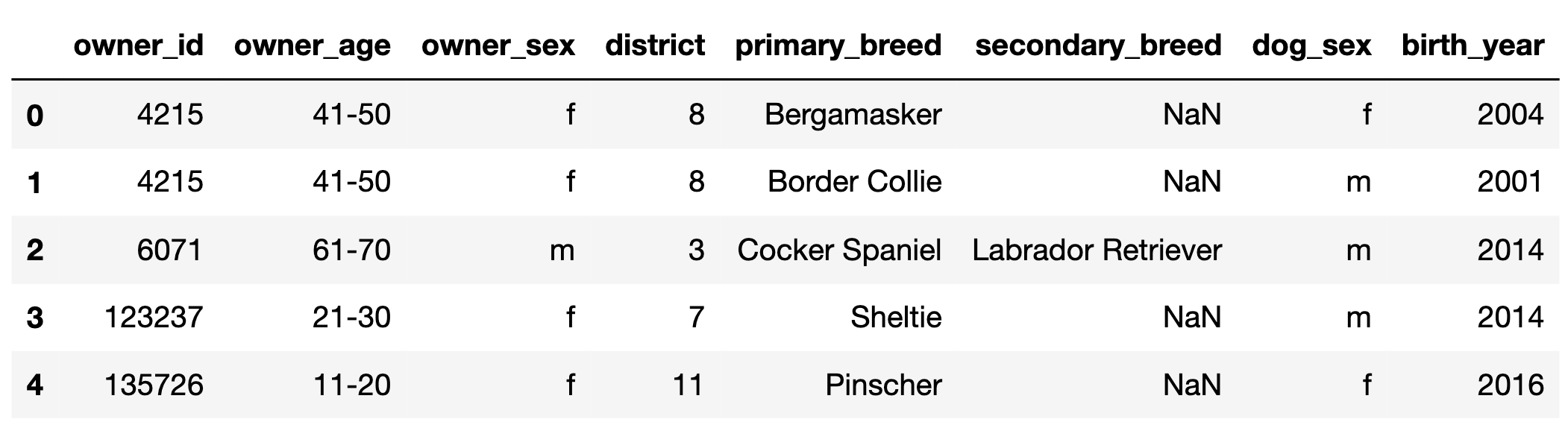
"owner_id" (int): A unique ID for each owner. Note
that, for example, there are two rows in the preview for
4215, meaning that owner has at least 2 dogs.
Assume that if an "owner_id" appears in
dogs multiple times, the corresponding
"owner_age", "owner_sex", and
"district" are always the same."owner_age" (str): The age group of the owner; either
"11-20", "21-30", …, or "91-100"
(9 possibilities in total)."owner_sex" (str): The birth sex of the owner; either
"m" (male) or "f" (female)."district" (int): The city district the owner lives in;
a positive integer between 1 and 12
(inclusive)."primary_breed" (str): The primary breed of the
dog."secondary_breed" (str): The secondary breed of the
dog. If this column is not null, the dog is a “mixed breed” dog;
otherwise, the dog is a “purebred” dog."dog_sex" (str): The birth sex of the dog; either
"m" (male) or "f" (female)."birth_year" (int): The birth year of the dog.In this question, assume that there are more than 12 districts in
dogs.
Suppose we merge the dogs DataFrame with itself as
follows.
# on="x" is the same as specifying both left_on="x" and right_on="x".
double = dogs.merge(dogs, on="district")
# sort_index sorts a Series in increasing order of its index.
square = double["district"].value_counts().value_counts().sort_index()The first few rows of square are shown below.
1 5500
4 215
9 40In dogs, there are 12 rows with a
"district" of 8. How many rows of
double have a "district" of 8?
Give your answer as a positive integer.
Answer: 144
When we merge dogs with dogs on
"district", each 8 in the first
dogs DataFrame will be combined with each 8 in
the second dogs DataFrame. Since there are 12 in the first
and 12 in the second, there are 12 \cdot 12 =
144 combinations.
What does the following expression evaluate to? Give your answer as a positive integer.
dogs.groupby("district").filter(lambda df: df.shape[0] == 3).shape[0]Hint: Unlike in 5.1, your answer to 5.2 depends on the values in
square.
Answer: 120
square is telling us that: - There are 5500 districts
that appeared just 1x in dogs. - There are 215 districts
that appeared 2x in dogs (2x, not 4x, because of the logic
explained in the 5a rubric item). - There are 40 districts that appeared
3x in dogs.
The expression given in this question is keeping all of the rows corresponding to districts that appear 3 times. There are 40 districts that appear 3 times. So, the total number of rows in this DataFrame is 40 \cdot 3 = 120.
Kyle and Yutong are trying to decide where they’ll study on campus and start flipping a Michigan-themed coin, with a picture of the Michigan Union on the heads side and a picture of the Shapiro Undergraduate Library (aka the UgLi) on the tails side.

Kyle flips the coin 21 times and sees 13 heads and 8 tails. He stores
this information in a DataFrame named kyle that has 21 rows
and 2 columns, such that:
The "flips" column contains "Heads" 13
times and "Tails" 8 times.
The "Markley" column contains "Kyle" 21
times.
Then, Yutong flips the coin 11 times and sees 4 heads and 7 tails.
She stores this information in a DataFrame named yutong
that has 11 rows and 2 columns, such that:
The "flips" column contains "Heads" 4
times and "Tails" 7 times.
The "MoJo" column contains "Yutong" 11
times.
How many rows are in the following DataFrame? Give your answer as an integer.
kyle.merge(yutong, on="flips")Hint: The answer is less than 200.
Answer: 108
Since we used the argument on="flips, rows from
kyle and yutong will be combined whenever they
have matching values in their "flips" columns.
For the kyle DataFrame:
"Heads" in the
"flips" column."Tails" in the
"flips" column.For the yutong DataFrame:
"Heads" in the
"flips" column."Tails" in the
"flips" column.The merged DataFrame will also only have the values
"Heads" and "Tails" in its
"flips" column.
"Heads" rows from kyle will each
pair with the 4 "Heads" rows from yutong. This
results in 13 \cdot 4 = 52 rows with
"Heads""Tails" rows from kyle will each
pair with the 7 "Tails" rows from yutong. This
results in 8 \cdot 7 = 56 rows with
"Tails".Then, the total number of rows in the merged DataFrame is 52 + 56 = 108.
Let A be your answer to the previous part. Now, suppose that:
kyle contains an additional row, whose
"flips" value is "Total" and whose
"Markley" value is 21.
yutong contains an additional row, whose
"flips" value is "Total" and whose
"MoJo" value is 11.
Suppose we again merge kyle and yutong on
the "flips" column. In terms of A, how many rows are in the new merged
DataFrame?
A
A+1
A+2
A+4
A+231
Answer: A+1
The additional row in each DataFrame has a unique
"flips" value of "Total". When we merge on the
"flips" column, this unique value will only create a single
new row in the merged DataFrame, as it pairs the "Total"
from kyle with the "Total" from
yutong. The rest of the rows are the same as in the
previous merge, and as such, they will contribute the same number of
rows, A, to the merged DataFrame. Thus,
the total number of rows in the new merged DataFrame will be A (from the original matching rows) plus 1
(from the new "Total" rows), which sums up to A+1.
For each day in May 2022, the DataFrame streams contains
the number of streams for each of the “Top 200" songs on Spotify that
day — that is, the number of streams for the 200 songs with the most
streams on Spotify that day. The columns in streams are as
follows:
"date": the date the song was streamed
"artist_names": name(s) of the artists who created
the song
"track_name": name of the song
"streams": the number of times the song was streamed
on Spotify that day
The first few rows of streams are shown below. Since
there were 31 days in May and 200 songs per day, streams
has 6200 rows in total.
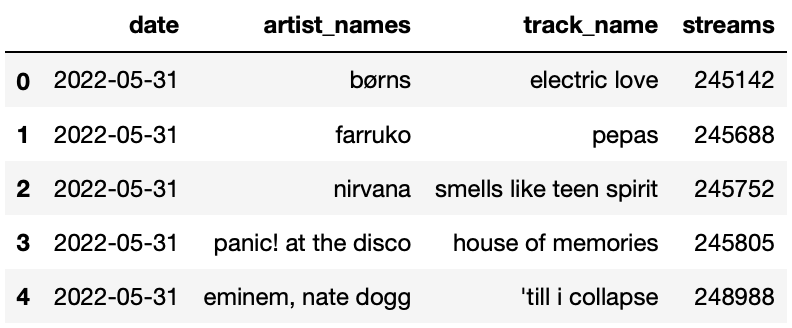
Note that:
streams is already sorted in a very particular way —
it is sorted by "date" in reverse chronological
(decreasing) order, and, within each "date", by
"streams" in increasing order.
Many songs will appear multiple times in streams,
because many songs were in the Top 200 on more than one day.
Suppose the DataFrame today consists of 15 rows — 3 rows
for each of 5 different "artist_names". For each artist, it
contains the "track_name" for their three most-streamed
songs today. For instance, there may be one row for
"olivia rodrigo" and "favorite crime", one row
for "olivia rodrigo" and "drivers license",
and one row for "olivia rodrigo" and
"deja vu".
Another DataFrame, genres, is shown below in its
entirety.
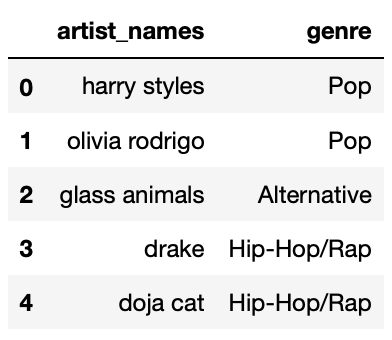
Suppose we perform an inner merge between
today and genres on
"artist_names". If the five "artist_names" in
today are the same as the five "artist_names"
in genres, what fraction of the rows in the merged
DataFrame will contain "Pop" in the "genre"
column? Give your answer as a simplified fraction.
Answer: \frac{2}{5}
If the five "artist_names" in today and
genres are the same, the DataFrame that results from an
inner merge will have 15 rows, one for each row in today.
This is because there are 3 matches for "harry styles", 3
matches for "olivia rodrigo", 3 matches for
"glass animals", and so on.
In the merged DataFrame’s 15 rows, 6 of them will correspond to
"Pop" artists — 3 to "harry styles" and 3 to
"olivia rodrigo". Thus, the fraction of rows that contain
"Pop" in the "genre" column is \frac{6}{15} = \frac{2}{5} (which is the
fraction of rows that contained "Pop" in
genres["genre"], too).
Suppose we perform an inner merge between
today and genres on
"artist_names". Furthermore, suppose that the only
overlapping "artist_names" between today and
genres are "drake" and
"olivia rodrigo". What fraction of the rows in the merged
DataFrame will contain "Pop" in the "genre"
column? Give your answer as a simplified fraction.
Answer: \frac{1}{2}
If we perform an inner merge, there will only be 6 rows in the merged
DataFrame — 3 for "olivia rodrigo" and 3 for
"drake". 3 of those 6 rows will have "Pop" in
the "genre" column, hence the answer is \frac{3}{6} = \frac{1}{2}.
Suppose we perform an outer merge between
today and genres on
"artist_names". Furthermore, suppose that the only
overlapping "artist_names" between today and
genres are "drake" and
"olivia rodrigo". What fraction of the rows in the merged
DataFrame will contain "Pop" in the "genre"
column? Give your answer as a simplified fraction.
Answer: \frac{2}{9}
Since we are performing an outer merge, we can decompose the rows in the merged DataFrame into three groups:
Rows that are in today that are not in
genres. There are 9 of these (3 each for the 3 artists that
are in today and not genres).
today doesn’t have a "genre" column, and so
all of these "genre"s will be NaN upon
merging.
Rows that are in genres that are not in
today. There are 3 of these — one for
"harry styles", one for "glass animals", and
one for "doja cat". 1 of these 3 have "Pop" in
the "genre" column.
Rows that are in both today and genres.
There are 6 of these — 3 for "olivia rodrigo" and 3 for
"drake" — and 3 of those rows contain "Pop" in
the "genre" column.
Tallying things up, we see that there are 9
+ 3 + 6 = 18 rows in the merged DataFrame overall, of which 0 + 1 + 3 = 4 have "Pop" in the
"genre" column. Hence, the relevant fraction is \frac{4}{18} = \frac{2}{9}.