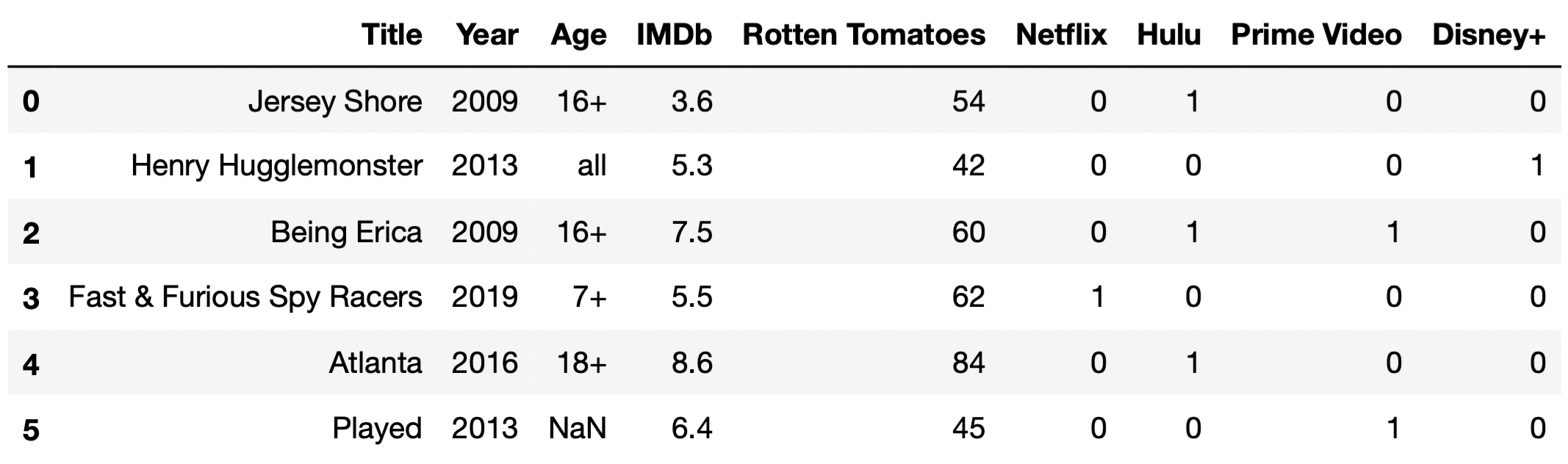
← return to study.practicaldsc.org
The problems in this worksheet are taken from past exams in similar
classes. Work on them on paper, since the exams you
take in this course will also be on paper.
We encourage you to
attempt these problems before Monday’s exam review
session, so that we have enough time to walk through the solutions to
all of the problems.
We will enable the solutions here after the
review session, though you can find the written solutions to these
problems in other discussion worksheets.
For this question, we will work with the DataFrame tv,
which contains information about various TV shows available to watch on
streaming services. For each TV show, we have:
"Title" (object): The title of the TV show."Year" (int): The year in which the TV show was first
released. (For instance, the show How I Met Your Mother ran
from 2005 to 2014; there is only one row for How I Met Your
Mother in tv, and its "Year" value is
2005.)"Age" (object): The age category for the TV show. If
not missing, "Age" is one of "all",
"7+", "13+", "16+", or
"18+". (For instance, "all" means that the
show is appropriate for all audiences, while `“18+”} means that the show
contains mature content and viewers should be at least 18 years
old.)"IMDb" (float): The TV show’s rating on IMDb (between 0
and 10)."Rotten Tomatoes" (int): The TV show’s rating on Rotten
Tomatoes (between 0 and 100)."Netflix" (int): 1 if the show is available for
streaming on Netflix and 0 otherwise. The "Hulu",
"Prime Video", and "Disney+" columns work the
same way.The first few rows of tv are shown below (though
tv has many more rows than are pictured here).
Assume that we have already run all of the necessary imports.
Throughout this problem, we will refer to tv
repeatedly.
In the following subparts, consider the variable
double_count, defined below.
double_count = tv["Title"].value_counts().value_counts()What is type(double_count)?
Series
SeriesGroupBy
DataFrame
DataFrameGroupBy
Answer: Series
The .value_counts() method, when called on a Series
s, produces a new Series in which
s.s.Since tv["Title"] is a Series,
tv["Title"].value_counts() is a Series, and so is
tv["Title"].value_counts.value_counts(). We provide an
interpretation of each of these Series in the solution to the next
subpart.
Which of the following statements are true? Select all that apply.
The only case in which it would make sense to set the index of
tv to "Title" is if
double_count.iloc[0] == 1 is True.
The only case in which it would make sense to set the index of
tv to "Title" is if
double_count.loc[1] == tv.shape[0] is
True.
If double_count.loc[2] == 5 is True, there
are 5 TV shows that all share the same "Title".
If double_count.loc[2] == 5 is True, there
are 5 pairs of 2 TV shows such that each pair shares the same
"Title".
None of the above.
Answers:
tv to "Title" is if
double_count.loc[1] == tv.shape[0] is
True.double_count.loc[2] == 5 is True, there
are 5 pairs of 2 TV shows such that each pair shares the same
"Title".To answer, we need to understand what each of
tv["Title"], tv["Title"].value_counts(), and
tv["Title"].value_counts().value_counts() contain. To
illustrate, let’s start with a basic, unrelated example. Suppose
tv["Title"] looks like:
0 A
1 B
2 C
3 B
4 D
5 E
6 A
dtype: objectThen, tv["Title"].value_counts() looks like:
A 2
B 2
C 1
D 1
E 1
dtype: int64and tv["Title"].value_counts().value_counts() looks
like:
1 3
2 2
dtype: int64Back to our actual dataset. tv["Title"], as we know,
contains the name of each TV show.
tv["Title"].value_counts() is a Series whose index is a
sequence of the unique TV show titles in tv["Title"], and
whose values are the frequencies of each title.
tv["Title"].value_counts() may look something like the
following:
Breaking Bad 1
Fresh Meat 1
Doctor Thorne 1
...
Styling Hollywood 1
Vai Anitta 1
Fearless Adventures with Jack Randall 1
Name: Title, Length: 5368, dtype: int64Then, tv["Title"].value_counts().value_counts() is a
Series whose index is a sequence of the unique values in the above
Series, and whose values are the frequencies of each value above. In the
case where all titles in tv["Title"] are unique, then
tv["Title"].value_counts() will only have one unique value,
1, repeated many times. Then,
tv["Title"].value_counts().value_counts() will only have
one row total, and will look something like:
1 5368
Name: Title, dtype: int64This allows us to distinguish between the first two answer choices. The key is remembering that in order to set a column to the index, the column should only contain unique values, since the goal of the index is to provide a “name” (more formally, a label) for each row.
tv to "Title" is if
double_count.iloc[0] == 1 is True”, is false.
As we can see in the example above, all titles are unique, but
double_count.iloc[0] is something other than 1.tv to "Title" is if
double_count.loc[1] == tv.shape[0] is True”,
is true. If double_count.loc[1] == tv.shape[0], it means
that all values in tv["Title"].value_counts() were 1,
meaning that tv["Title"] consisted solely of unique values,
which is the only case in which it makes sense to set
"Title" to the index.Now, let’s look at the second two answer choices. If
double_counts.loc[2] == 5, it would mean that 5 of the
values in tv["Title"].value_counts() were 2. This would
mean that there were 5 pairs of titles in tv["Title"] that
were the same.
double_count.loc[2] == 5 is True, there are 5
pairs of 2 TV shows such that each pair shares the same
"Title"”, correct.double_count.loc[2] == 5
is True, there are 5 TV shows that all share the same
"Title"”, is incorrect; if there were 5 TV shows with the
same title, then double_count.loc[5] would be at least 1,
but we can’t make any guarantees about
double_counts.loc[2].Ethan is an avid Star Wars fan, and the only streaming service he has an account on is Disney+. (He had a Netflix account, but then Netflix cracked down on password sharing.)
Fill in the blanks below so that star_disney_prop
evaluates to the proportion of TV shows in tv with
"Star Wars" in the title that are available to stream on
Disney+.
star_only = __(a)__
star_disney_prop = __(b)__ / star_only.shape[0]What goes in the blanks?
Answers:
tv[tv["Title"].str.contains("Star Wars")]star_only["Disney+"].sum()We’re asked to find the proportion of TV shows with
"Star Wars" in the title that are available to stream on
Disney+. This is a fraction, where:
"Star Wars" in the title and are available
to stream on Disney+."Star Wars" in the title.The key is recognizing that star_only must be a
DataFrame that contains all the rows in which the "Title"
contains "Star Wars"; to create this DataFrame in blank
(a), we use tv[tv["Title"].str.contains("Star Wars")].
Then, the denominator is already provided for us, and all we need to
fill in is the numerator. There are a few possibilities, though they all
include star_only:
star_only["Disney+"].sum()(star_only["Disney+"] == 1).sum()star_only[star_only["Disney+"] == 1].shape[0]Common misconception: Many students calculated the
wrong proportion: they calculated the proportion of shows available to
stream on Disney+ that have "Star Wars" in the title. We
asked for the proportion of shows with "Star Wars" in the
title that are available to stream on Disney+; “proportion of X that Y” is
always \frac{\# X \text{ and } Y}{\#
X}.
In this problem, we will be using the following DataFrame
students, which contains various information about high
school students and the university/universities they applied to.
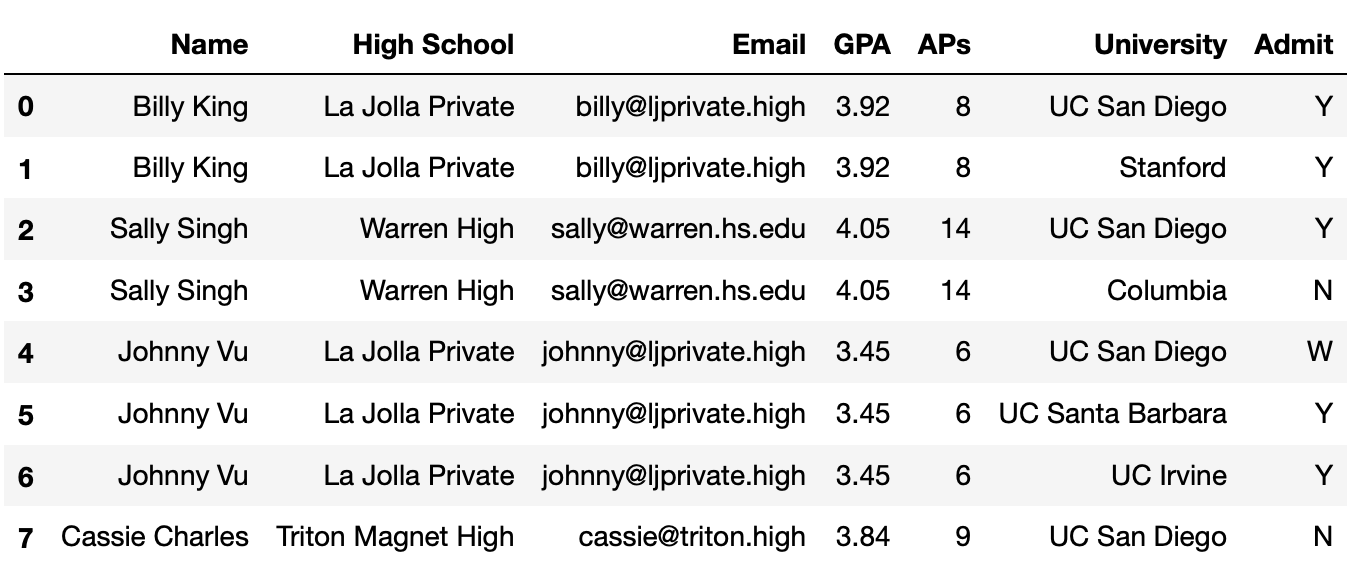
The columns are:
'Name' (str): the name of the student.'High School' (str): the High School that the student
attended.'Email' (str): the email of the student.'GPA' (float): the GPA of the student.'AP' (int): the number of AP exams that the student
took.'University' (str): the name of the university that the
student applied to.'Admit' (str): the acceptance status of the student
(where ‘Y’ denotes that they were accepted to the university and ‘N’
denotes that they were not).The rows of 'student' are arranged in no particular
order. The first eight rows of 'student' are shown above
(though 'student' has many more rows than pictured
here).
Fill in the blank so that the result evaluates to a Series indexed by
"Email" that contains a list of the
universities that each student was admitted to. If a
student wasn’t admitted to any universities, they should have an empty
list.
students.groupby("Email").apply(_____)What goes in the blank?
Answer:
lambda df: df.loc[df["Admit"] == "Y", "University"].tolist()
Which of the following blocks of code correctly assign
max_AP to the maximum number of APs taken by a student who
was rejected by UC San Diego?
Option 1:
cond1 = students["Admit"] == "N"
cond2 = students["University"] == "UC San Diego"
max_AP = students.loc[cond1 & cond2, "APs"].sort_values().iloc[-1]Option 2:
cond1 = students["Admit"] == "N"
cond2 = students["University"] == "UC San Diego"
d3 = students.groupby(["University", "Admit"]).max().reset_index()
max_AP = d3.loc[cond1 & cond2, "APs"].iloc[0]Option 3:
p = students.pivot_table(index="Admit",
columns="University",
values="APs",
aggfunc="max")
max_AP = p.loc["N", "UC San Diego"]Option 4:
# .last() returns the element at the end of a Series it is called on
groups = students.sort_values(["APs", "Admit"]).groupby("University")
max_AP = groups["APs"].last()["UC San Diego"]Select all that apply. There is at least one correct option.
Option 1
Option 2
Option 3
Option 4
Answer: Option 1 and Option 3
Option 1 works correctly, it is probably the most straightforward
way of answering the question. cond1 is True
for all rows in which students were rejected, and cond2 is
True for all rows in which students applied to UCSD. As
such, students.loc[cond1 & cond2] contains only the
rows where students were rejected from UCSD. Then,
students.loc[cond1 & cond2, "APs"].sort_values() sorts
by the number of "APs" taken in increasing order, and
.iloc[-1] gets the largest number of "APs"
taken.
Option 2 doesn’t work because the lengths of cond1
and cond2 are not the same as the length of
d3, so this causes an error.
Option 3 works correctly. For each combination of
"Admit" status ("Y", "N",
"W") and "University" (including UC San
Diego), it computes the max number of "APs". The usage of
.loc["N", "UC San Diego"] is correct too.
Option 4 doesn’t work. It currently returns the maximum number of
"APs" taken by someone who applied to UC San Diego; it does
not factor in whether they were admitted, rejected, or
waitlisted.
Currently, students has a lot of repeated information —
for instance, if a student applied to 10 universities, their GPA appears
10 times in students.
We want to generate a DataFrame that contains a single row for each
student, indexed by "Email", that contains their
"Name", "High School", "GPA", and
"APs".
One attempt to create such a DataFrame is below.
students.groupby("Email").aggregate({"Name": "max",
"High School": "mean",
"GPA": "mean",
"APs": "max"})There is exactly one issue with the line of code above. In one sentence, explain what needs to be changed about the line of code above so that the desired DataFrame is created.
Answer: The problem right now is that aggregating
High School by mean doesn’t work since you can’t aggregate a column with
strings using "mean". Thus changing it to something that
works for strings like "max" or "min" would
fix the issue.
Consider the following snippet of code.
pivoted = students.assign(Admit=students["Admit"] == "Y") \
.pivot_table(index="High School",
columns="University",
values="Admit",
aggfunc="sum")Some of the rows and columns of pivoted are shown
below.
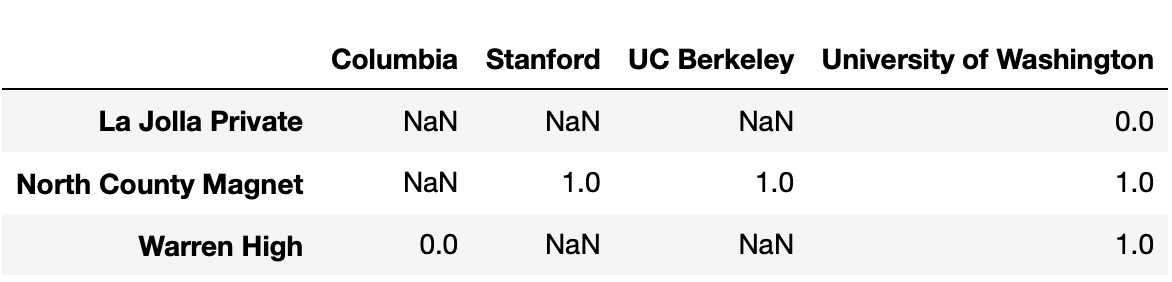
No students from Warren High were admitted to Columbia or Stanford.
However,
pivoted.loc["Warren High", "Columbia"] and
pivoted.loc["Warren High", "Stanford"] evaluate to
different values. What is the reason for this difference?
Some students from Warren High applied to Stanford, and some others applied to Columbia, but none applied to both.
Some students from Warren High applied to Stanford but none applied to Columbia.
Some students from Warren High applied to Columbia but none applied to Stanford.
The students from Warren High that applied to both Columbia and Stanford were all rejected from Stanford, but at least one was admitted to Columbia.
When using pivot_table, pandas was not able
to sum strings of the form "Y", "N", and
"W", so the values in pivoted are
unreliable.
Answer: Option 3
pivoted.loc["Warren High", "Stanford"] is
NaN because there were no rows in students in
which the "High School" was "Warren High" and
the "University" was "Stanford", because
nobody from Warren High applied to Stanford. However,
pivoted.loc["Warren High", "Columbia"] is not
NaN because there was at least one row in
students in which the "High School" was
"Warren High" and the "University" was
"Columbia". This means that at least one student from
Warren High applied to Columbia.
Option 3 is the only option consistent with this logic.
After taking the SAT, Nicole wants to check the College Board’s website to see her score. However, the College Board recently updated their website to use non-standard HTML tags and Nicole’s browser can’t render it correctly. As such, she resorts to making a GET request to the site with her scores on it to get back the source HTML and tries to parse it with BeautifulSoup.
Suppose soup is a BeautifulSoup object instantiated
using the following HTML document.
<college>Your score is ready!</college>
<sat verbal="ready" math="ready">
Your percentiles are as follows:
<scorelist listtype="percentiles">
<scorerow kind="verbal" subkind="per">
Verbal: <scorenum>84</scorenum>
</scorerow>
<scorerow kind="math" subkind="per">
Math: <scorenum>99</scorenum>
</scorerow>
</scorelist>
And your actual scores are as follows:
<scorelist listtype="scores">
<scorerow kind="verbal"> Verbal: <scorenum>680</scorenum> </scorerow>
<scorerow kind="math"> Math: <scorenum>800</scorenum> </scorerow>
</scorelist>
</sat>Which of the following expressions evaluate to "verbal"?
Select all that apply.
soup.find("scorerow").get("kind")
soup.find("sat").get("ready")
soup.find("scorerow").text.split(":")[0].lower()
[s.get("kind") for s in soup.find_all("scorerow")][-2]
soup.find("scorelist", attrs={"listtype":"scores"}).get("kind")
None of the above
Answer: Option 1, Option 3, Option 4
Correct options:
<scorerow> element and
retrieves its "kind" attribute, which is
"verbal" for the first <scorerow>
encountered in the HTML document.<scorerow> tag,
retrieves its text ("Verbal: 84"), splits this text by “:”,
and takes the first element of the resulting list
("Verbal"), converting it to lowercase to match
"verbal"."kind" attributes for all
<scorerow> elements. The second to last (-2) element
in this list corresponds to the "kind" attribute of the
first <scorerow> in the second
<scorelist> tag, which is also
"verbal".Incorrect options:
<sat> tag, which does not exist as an attribute."kind" attribute from a
<scorelist> tag, but <scorelist>
does not have a "kind" attribute.Consider the following function.
def summer(tree):
if isinstance(tree, list):
total = 0
for subtree in tree:
for s in subtree.find_all("scorenum"):
total += int(s.text)
return total
else:
return sum([int(s.text) for s in tree.find_all("scorenum")])For each of the following values, fill in the blanks to assign
tree such that summer(tree) evaluates to the
desired value. The first example has been done for you.
84 tree = soup.find("scorerow")183 tree = soup.find(__a__)1480 tree = soup.find(__b__)899 tree = soup.find_all(__c__)Answer: a: "scorelist", b:
"scorelist", attrs={"listtype":"scores"}, c:
"scorerow", attrs={"kind":"math"}
soup.find("scorelist") selects the first
<scorelist> tag, which includes both verbal and math
percentiles (84 and 99). The function
summer(tree) sums these values to get 183.
This selects the <scorelist> tag with
listtype="scores", which contains the actual scores of
verbal (680) and math (800). The function sums
these to get 1480.
This selects all <scorerow>elements with
kind="math", capturing both the percentile
(99) and the actual score (800). Since tree is
now a list, summer(tree) iterates through each
<scorerow> in the list, summing their
<scorenum> values to reach 899.
The EECS 398 staff are looking into hotels — some in San Diego, for their family to stay at for graduation (and to eat Mexican food), and some elsewhere, for summer trips.
Each row of hotels contains information about a
different hotel in San Diego. Specifically, for each hotel, we have:
"Hotel Name" (str): The name of the hotel.
Assume hotel names are unique."Location" (str): The hotel’s neighborhood in San
Diego."Chain" (str): The chain the hotel is a part of; either
"Hilton", "Marriott", "Hyatt", or "Other". A hotel chain is
a group of hotels owned or operated by a shared company."Number of Rooms" (int): The number of rooms the hotel
has.The first few rows of hotels are shown below, but hotels
has many more rows than are shown.
Now, consider the variable summed, defined below.
summed = hotels.groupby("Chain")["Number of Rooms"].sum().idxmax()What is type(summed)?
int
str
Series
DataFrame
DataFrameGroupBy
Answer: str
When we do a groupby on the Chain column in
hotels, this means that the values in the
Chain column will be the indices of the DataFrame or Series
we get as output, in this case the Series
hotels.groupby("Chain")["Number of Rooms"].sum().
Since the values of Chain are strings, and since
.idxmax() will return a value from the index of the
aforementioned Series, summed is a string.
In one sentence, explain what the value of summed means.
Phrase your explanation as if you had to give it to someone who is not a
data science major; that is, don’t say something like “it is the result
of grouping hotels by "Chain", selecting the
"Number of Rooms" column, …”, but instead, give the value
context.
Answer: summed is the name of the hotel
chain with the most total rooms
The result of the .groupby() and .sum() is
a Series indexed by the unique Chains, whose values are the
total number of rooms in hotels owned by each chain. The
idxmax() function gets the index corresponding to the
largest value in the Series, which will be the hotel chain name with the
most total rooms.
Consider the variable curious, defined below.
curious = frame["Chain"].value_counts().idxmax()Fill in the blank: curious is guaranteed to be equal to
summed only if frame has one row for every
____ in San Diego.
hotel
hotel chain
hotel room
neighborhood
Answer: hotel room
curious gets the most common value of Chain
in the DataFrame frame. We already know that
summed is the hotel chain with the most rooms in San Diego,
so curious only equals summed if the most
common Chain in frame is the hotel chain with
the most total rooms; this occurs when each row of frame is
a single hotel room.
Fill in the blanks so that popular_areas is an array of
the names of the unique neighborhoods that have at least 5 hotels and at
least 1000 hotel rooms.
f = lambda df: __(i)__
popular_areas = (hotels
.groupby(__(ii)__)
.__(iii)__
__(iv)__)What goes in blank (i)?
What goes in blank (ii)?
"Hotel Name"
"Location"
"Chain"
"Number of Rooms"
agg(f)
filter(f)
transform(f)
Answers:
df.shape[0] >= 5 and df["Number of Rooms"].sum() >= 1000"Location"filter(f)["Location"].unique() or equivalentWe’d like to only consider certain neighborhoods according to group
characteristics (having >= 5 hotels and >= 1000 hotel rooms), and
.filter() allows us to do that by excluding groups not
meeting those criteria. So, we can write a function that evaluates those
criteria on one group at a time (the df of input to
f is the subset of hotels containing just one
Location value), and calling filter(f) means
that the only remaining rows are hotels in neighborhoods that match
those criteria. Finally, all we have to do is get the unique
neighborhoods from this DataFrame, which are the neighborhoods for which
f returned True.
Consider the code below.
cond1 = hotels["Chain"] == "Marriott"
cond2 = hotels["Location"] == "Coronado"
combined = hotels[cond1].merge(hotels[cond2], on="Hotel Name", how=???)??? with "inner" in the code
above, which of the following will be equal to
combined.shape[0]? min(cond1.sum(), cond2.sum())
(cond1 & cond2).sum()
cond1.sum() + cond2.sum()
cond1.sum() + cond2.sum() - (cond1 & cond2).sum()
cond1.sum() + (cond1 & cond2).sum()
??? with "outer" in the code
above, which of the following will be equal to
combined.shape[0]? min(cond1.sum(), cond2.sum())
(cond1 & cond2).sum()
cond1.sum() + cond2.sum()
cond1.sum() + cond2.sum() - (cond1 & cond2).sum()
cond1.sum() + (cond1 & cond2).sum()
Answers:
(cond1 & cond2).sum()cond1.sum() + cond2.sum() - (cond1 & cond2).sum()Note that cond1 and cond2 are boolean
Series, and hotels[cond1] and hotels[cond2]
are the subsets of hotels where
Chain == "Marriott and
"Location" == "Coronado", respectively.
When we perform an inner merge, we’re selecting every row where a
Hotel Name appears in both
hotels[cond1] and hotels[cond2]. This is the
same set of indices (and therefore hotel names, since those are unique)
as where (cond1 & cond2) == True. So, the length of
combined will be the same as the number of
Trues in (cond1 & cond2).
When we perform an outer merge, we’re selecting every row that
appears in either DataFrame, although there will not be repeats
for hotels that are both Marriott properties and are in Coronado. So, to
find the total number of rows in either DataFrame, we take the sum of
the sizes of each, and subtract rows that appear in both, which
corresponds to answer
cond1.sum() + cond2.sum() - (cond1 & cond2).sum().
Pranavi proposes the following imputation scheme.
def impute(s):
return s.fillna(np.random.choice(s[s.notna()]))True or False: impute performs
probabilistic imputation, using the same definition of probabilistic
imputation we learned about in class.
True
False
Answer: False
In impute, np.random.choice will return a
single non-null value from s, and .fillna()
will fill every null value with this single value. Meanwhile,
probabilistic imputation draws a different value from a specified
distribution to fill each missing value, making it such that there won’t
be a single “spike” in the imputed distribution at a single chosen
value.
Consider the following expressions and values.
>>> vals.isna().mean()
0.2
>>> vals.describe().loc[["min", "mean", "max"]]
min 2.0
mean 4.0
max 7.0
dtype: float64Given the above, what is the maximum possible value
of impute(vals).mean()? Give your answer as a number
rounded to one decimal place.
Answer: 4.6
The maximum possible value of impute(vals).mean() would
occur when every single missing value in vals is filled in
with the highest possible non-null value in vals. (As
discussed in the previous solution, impute selects only one
value from s to fill into every missing space.)
If this occurs, then the mean of the imputed Series will be weighted mean of the available data and the filled data, and given the numbers in the question, this is 0.8 \cdot 4 + 0.2 \cdot 7, or 4.6.
Which of the following statements below will always evaluate to
True?
vals.std() < impute(vals).std()
vals.std() <= impute(vals).std()
vals.std() == impute(vals).std()
vals.std() >= impute(vals).std()
vals.std() > impute(vals).std()
None of the above
Answer: None of the above
Since the value which impute will choose to impute with
is random, the effect that it has on the standard deviation of
vals is unknown. If the missing values are filled with a
value close to the mean, this could reduce standard deviation; if they
are filled with a value far from the mean, this could increase standard
deviation. (Of course, the imputation will also shift the mean, so
without knowing details of the Series, it’s impossible to come up with
thresholds.) In any case, since the value for imputation is chosen at
random, none of these statements will always be true, and so
the correct answer is “none of the above.”