
← return to study.practicaldsc.org
The problems in this worksheet are taken from past exams in similar
classes. Work on them on paper, since the exams you
take in this course will also be on paper.
We encourage you to
attempt these problems before Tuesday’s exam review
session, so that we have enough time to walk through the solutions to
all of the problems.
We will enable the solutions here after the
review session, though you can find the written solutions to these
problems in other discussion worksheets.
Consider a dataset of n values, y_1, y_2, ..., y_n, all of which are non-negative. We’re interested in fitting a constant model, H(x) = h, to the data, using the new “Wolverine” loss function:
L_\text{wolverine}(y_i, h) = w_i \left( y_i^2 - h^2 \right)^2
Here, w_i corresponds to the “weight” assigned to the data point y_i, the idea being that different data points can be weighted differently when finding the optimal constant prediction, h^*.
For example, for the dataset y_1 = 1, y_2 = 5, y_3 = 2, we will end up with different values of h^* when we use the weights w_1 = w_2 = w_3 = 1 and when we use weights w_1 = 8, w_2 = 4, w_3 = 3.
Find \frac{\partial L_\text{wolverine}}{\partial h}, the derivative of the Wolverine loss function with respect to h. Show your work.
\frac{\partial L}{\partial h} = -4w_ih(y_i^2 -h^2)
To solve this problem we simply take the derivative of L_\text{wolverine}(y_i, h) = w_i( y_i^2 - h^2 )^2.
We can use the chain rule to find the derivative. The chain rule is: \frac{\partial}{\partial h}[f(g(h))]=f'(g(h))g'(h).
Note that (y_i^2 -h^2)^2 is the area we care about inside of L_\text{wolverine}(y_i, h) = w_i( y_i^2 - h^2 )^2 because that is where h is!. In this case f(h) = h^2 and g(h) = y_i^2 - h^2. We can then take the derivative of both to get: f'(h) = 2h and g'(x) = -2h.
This tells us the derivative is: \frac{\partial L}{\partial h} = (w_i) * 2(y_i^2 -h^2) * (-2h), which can be simplified to \frac{\partial L}{\partial h} = -4w_ih(y_i^2 -h^2).
Prove that the constant prediction that minimizes average loss for the Wolverine loss function is:
h^* = \sqrt{\frac{\sum_{i = 1}^n w_i y_i^2}{\sum_{i = 1}^n w_i}}
The recipe for average loss is to find the derivative of the risk function, set it equal to zero, and solve for h^*.
We know that average loss follows the equation R(L(y_i, h)) = \frac{1}{n} \sum_{i=1}^n L(y_i, h). This means that R_\text{wolverine}(h) = \frac{1}{n} \sum_{i = 1}^n w_i (y_i^2 - h^2)^2.
Recall we have already found the derivative of L_\text{wolverine}(y_i, h) = w_i ( y_i^2 - h^2)^2. Which means that \frac{\partial R}{\partial h}(h) = \frac{1}{n} \sum_{i = 1}^n \frac{\partial L}{\partial h}(h). So we can set \frac{\partial}{\partial h}(h) R_\text{wolverine}(h) = \frac{1}{n} \sum_{i = 1}^n -4hw_i(y_i^2 -h^2).
We can now do the last two steps: \begin{align*} 0 &= \frac{1}{n} \sum_{i = 1}^n -4hw_i(y_i^2 -h^2)\\ 0&= \frac{-4h}{n} \sum_{i = 1}^n w_ih(y_i^2 -h^2)\\ 0&= \sum_{i = 1}^n w_i(y_i^2 -h^2)\\ 0&= \sum_{i = 1}^n w_iy_i^2 -w_ih^2\\ 0&= \sum_{i = 1}^n w_iy_i^2 - \sum_{i = 1}^n w_ih^2\\ \sum_{i = 1}^n w_ih^2 &= \sum_{i = 1}^n w_iy_i^2\\ h^2\sum_{i = 1}^n w_i &= \sum_{i = 1}^n w_iy_i^2\\ h^2 &= \frac{\sum_{i = 1}^n w_iy_i^2}{\sum_{i = 1}^n w_i}\\ h^* &= \sqrt{\frac{\sum_{i = 1}^n w_iy_i^2}{\sum_{i = 1}^n w_i}} \end{align*}
For a dataset of non-negative values y_1, y_2, ..., y_n with weights w_1, 1, ..., 1, evaluate: \displaystyle \lim_{w_1 \rightarrow \infty} h^*
The maximum of y_1, y_2, ..., y_n
The mean of y_1, y_2, ..., y_{n-1}
The mean of y_2, y_3, ..., y_n
The mean of y_2, y_3, ..., y_n, multiplied by \frac{n}{n-1}
y_1
y_n
y_1
Recall from part b h^* = \sqrt{\frac{\sum_{i = 1}^n w_i y_i^2}{\sum_{i = 1}^n w_i}}.
The problem is asking us \lim_{w_1 \rightarrow \infty} \sqrt{\frac{\sum_{i = 1}^n w_i y_i^2}{\sum_{i = 1}^n w_i}}.
We can further rewrite the problem to get something like this: \lim_{w_1 \rightarrow \infty} \sqrt{\frac{w_1 y_1^2 + \sum_{i=1}^{n-1}y_i^2}{w_1 + (n-1)}}. Note that \frac{\sum_{i=1}^{n-1}y_i^2}{n-1} is insignificant because it is a constant. Constants compared to infinity can be ignored. We now have something like \sqrt{\frac{w_1y_1^2}{w_1}}. We can cancel out the w_1 to get \sqrt{y_1^2}, which becomes y_1.
Suppose we want to fit a hypothesis function of the form:
H(x_i) = w_0 + w_1 x_i^2
Note that this is not the simple linear regression hypothesis function, H(x_i) = w_0 + w_1x_i.
To do so, we will find the optimal parameter vector \vec{w}^* = \begin{bmatrix} w_0^* \\ w_1^* \end{bmatrix} that satisfies the normal equations. The first 5 rows of our dataset are as follows, though note that our dataset has n rows in total.
| x | y |
|---|---|
| 2 | 4 |
| -1 | 4 |
| 3 | 4 |
| -7 | 4 |
| 3 | 4 |
Suppose that x_1, x_2, ..., x_n have a mean of \bar{x} = 2 and a variance of \sigma_x^2 = 10.
Write out the first 5 rows of the design matrix, X.
Answer: X = \begin{bmatrix} 1 & 4 \\ 1 & 1 \\ 1 & 9 \\ 1 & 49 \\ 1 & 9 \end{bmatrix}
Recall our hypothesis function is H(x_i) = w_0 + w_1x_i^2. Since there is an intercept term present, and w_0 is the first parameter, the first column of our design matrix will be all 1s. Our second column should contain x_1^2, x_2^2, ..., x_n^2. This means we take each datapoint x_i and square it to form the second column of X.
Suppose, just in part (b), that after solving the normal equations, we find \vec{w}^* = \begin{bmatrix} 2 \\ -5 \end{bmatrix}. What is the predicted y value for x = 2? Give your answer as an integer with no variables. Show your work.
Answer: -18
(2)(1)+(-5)(4)=-18
To find the predicted y value, we plug in x_i = 2 into the hypothesis function H(x_i) = w_0 + w_1x_i^2, or take the dot product of \vec{w}^* with \begin{bmatrix}1 \\ 2^2\end{bmatrix}.
\begin{align*} &\begin{bmatrix} 2 \\ -5 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 4 \end{bmatrix}\\ &(2)(1)+(-5)(4)\\ &2 - 20\\ &-18 \end{align*}
Let X_\text{tri} = 3 X. Using the fact that \sum_{i = 1}^n x_i^2 = n \sigma_x^2 + n \bar{x}^2, determine the value of the bottom-left value in the matrix X_\text{tri}^T X_\text{tri}, i.e. the value in the second row and first column. Give your answer as an expression involving n. Show your work.
Answer: 126n
X = \begin{bmatrix} 1 & x_1^2 \\ 1 & x_2^2 \\ \vdots & \vdots \\ 1 & x_n^2 \end{bmatrix}
X_{\text{tri}} = \begin{bmatrix} 3 & 3x_1^2 \\ 3 & 3x_2^2 \\ \vdots & \vdots \\ 3 & 3x_n^2 \end{bmatrix}
We want to know what the bottom left value of X_\text{tri}^T X_\text{tri} is. We figure this out with matrix multiplication!
\begin{align*} X_\text{tri}^T X_\text{tri} &= \begin{bmatrix} 3 & 3 & ... & 3\\ 3x_1^2 & 3x_2^2 & ... & 3x_n^2 \end{bmatrix} \begin{bmatrix} 3 & 3x_1^2 \\ 3 & 3x_2^2 \\ \vdots & \vdots \\ 3 & 3x_n^2 \end{bmatrix}\\ &= \begin{bmatrix} \sum_{i = 1}^n 3(3) & \sum_{i = 1}^n 3(3x_i^2) \\ \sum_{i = 1}^n 3(3x_i^2) & \sum_{i = 1}^n (3x_i^2)(3x_i^2)\end{bmatrix}\\ &= \begin{bmatrix} \sum_{i = 1}^n 9 & \sum_{i = 1}^n 9x_i^2 \\ \sum_{i = 1}^n 9x_i^2 & \sum_{i = 1}^n (3x_i^2)^2 \end{bmatrix} \end{align*}
We can see that the bottom left element should be \sum_{i = 1}^n 9x_i^2.
From here we can use the fact given to us in the directions: \sum_{i = 1}^n x_i^2 = n \sigma_x^2 + n \bar{x}^2.
\begin{align*} \sum_{i = 1}^n 9x_i^2 &= 9\sum_{i = 1}^n x_i^2\\ &= 9(n \sigma_x^2 + n \bar{x}^2)\\ &= 9(10n + 2^2n)\\ &= 9(10n + 4n)\\ &= 9(14n) = 126n \end{align*}
Suppose we have one qualitative variable that that we convert to numerical values using one- hot encoding. We’ve shown the first four rows of the resulting design matrix below:

Say we train a linear model m_1 on these data. Then, we replace all of the 1 values in column a with 3’s and all of the 1 values in column b with 2’s and train a new linear model m_2. Neither m_1 nor m_2 have an intercept term. On the training data, the average squared loss for m_1 will be ________ that of m_2.
greater than
less than
equal to
impossible to tell
Answers:
The answer is equal to.
Because we can simply adjust the weights in the opposite way that we rescale the one-hot columns, any model obtainable with the original encoding can also be obtained with the rescaled encoding. This guarantees that the training loss remains unchanged.
When one-hot encoding is used, each category is represented by a column that typically contains only 0s and 1s. Rescaling these columns means multiplying the 1s by a constant (for example, turning 1 into 2 or 3). However, if we also adjust the corresponding weights in the model by dividing by that same constant, the product of the rescaled column value and its weight remains the same. Since the model’s predictions are based on these products, the predictions will not change, and as a result, the average squared loss on the training data will also remain unchanged.
For example, let us say we have categorical variable “Color” with three levels: Red, Green, and Blue. We one-hot encode this variable into three columns. For an observation: - If the color is Red, the encoded values might be: Red = 1, Green = 0, Blue = 0.
Now, suppose we decide to multiply the column for Red by 2. The new value for a Red observation becomes 2 instead of 1. To keep the prediction the same, we can simply use half the weight for this column in the model. This inverse adjustment ensures that the final product (column value multiplied by weight) remains unchanged. Thus, the model’s prediction and the average squared loss on the training data stay the same.
To account for the intercept term, we add a column of all ones to our design matrix from part a. That is, the resulting design matrix has four columns: a with 3’s instead of 1’s, b with 2’s instead of 1’s, c, and a column of all ones. What is the rank of the new design matrix with these four columns?
1
2
3
4
Answers:
The answer is 3.
Note that the column c = intercept column −\frac{1}{3}a + \frac{1}{2}b. Hence, there is a linear dependence relationship, meaning that one of the columns is redundant and that the rank of the new design matrix is 3.
One piece of information that may be useful as a feature is the
proportion of SAT test takers in a state in a given year that qualify
for free lunches in school. The Series lunch_props contains
8 values, each of which are either "low",
"medium", or "high". Since we can’t use
strings as features in a model, we decide to encode these strings using
the following Pipeline:
# Note: The FunctionTransformer is only needed to change the result
# of the OneHotEncoder from a "sparse" matrix to a regular matrix
# so that it can be used with StandardScaler;
# it doesn't change anything mathematically.
pl = Pipeline([
("ohe", OneHotEncoder(drop="first")),
("ft", FunctionTransformer(lambda X: X.toarray())),
("ss", StandardScaler())
])After calling pl.fit(lunch_props),
pl.transform(lunch_props) evaluates to the following
array:
array([[ 1.29099445, -0.37796447],
[-0.77459667, -0.37796447],
[-0.77459667, -0.37796447],
[-0.77459667, 2.64575131],
[ 1.29099445, -0.37796447],
[ 1.29099445, -0.37796447],
[-0.77459667, -0.37796447],
[-0.77459667, -0.37796447]])and pl.named_steps["ohe"].get_feature_names() evaluates
to the following array:
array(["x0_low", "x0_med"], dtype=object)Given the above information, we can conclude that
lunch_props has (a) value(s) equal to
"low", (b) value(s) equal to
"medium", and (c) value(s) equal to
"high". (Note: You should write one positive integer in
each box such that the numbers add up to 8.)
What are (a), (b), and (c)? Give you answers as positive integers.
Answer: 3, 1, 4
The first column of the transformed array corresponds to the
standardized one-hot-encoded low column. There are 3 values
that are positive, which means there are 3 values that were originally
1 in that column pre-standardization. This means that 3 of
the values in lunch_props were originally
"low".
The second column of the transformed array corresponds to the
standardized one-hot-encoded med column. There is only 1
value in the transformed column that is positive, which means only 1 of
the values in lunch_props was originally
"medium".
The Series lunch_props has 8 values, 3 of which were
identified as "low" in subpart 1, and 1 of which was
identified as "medium" in subpart 2. The number of values
being "high" must therefore be 8
- 3 - 1 = 4.
Consider the least squares regression model, \vec{h} = X \vec{w}. Assume that X and \vec{h} refer to the design matrix and hypothesis vector for our training data, and \vec y is the true observation vector.
Let \vec{w}_\text{OLS}^* be the parameter vector that minimizes mean squared error without regularization. Specifically:
\vec{w}_\text{OLS}^* = \arg\underset{\vec{w}}{\min} \frac{1}{n} \| \vec{y} - X \vec{w} \|^2_2
Let \vec{w}_\text{ridge}^* be the parameter vector that minimizes mean squared error with L_2 regularization, using a non-negative regularization hyperparameter \lambda (i.e. ridge regression). Specifically:
\vec{w}_\text{ridge}^* = \arg\underset{\vec{w}}{\min} \frac{1}{n} \| \vec y - X \vec{w} \|^2_2 + \lambda \sum_{j=1}^{p} w_j^2
For each of the following problems, fill in the blank.
If we set \lambda = 0, then \Vert \vec{w}_\text{OLS}^* \Vert^2_2 is ____ \Vert \vec{w}_\text{ridge}^* \Vert^2_2
less than
equal to
greater than
impossible to tell
Answers:
equal to
For each of the remaining parts, you can assume that \lambda is set such that the predicted response vectors for our two models (\vec{h} = X \vec{w}_\text{OLS}^* and \vec{h} = X \vec{w}_\text{ridge}^*) is different.
The training MSE of the model \vec{h} = X \vec{w}_\text{OLS}^* is ____ than the model \vec{h} = X \vec{w}_\text{ridge}^*.
less than
equal to
greater than
impossible to tell
Answers:
less than
Now, assume we’ve fit both models using our training data, and evaluate both models on some unseen testing data.
The test MSE of the model \vec{h} = X \vec{w}_\text{OLS}^* is ____ than the model \vec{h} = X \vec{w}_\text{ridge}^*.
less than
equal to
greater than
impossible to tell
Answers:
impossible to tell
Assume that our design matrix X contains a column of all ones. The sum of the residuals of our model \vec{h} = X \vec{w}_\text{ridge}^* ____.
equal to 0
not necessarily equal to 0
Answers:
not necessarily equal to 0
As we increase \lambda, the bias of the model \vec{h} = X \vec{w}_\text{ridge}^* tends to ____.
increase
stay the same
decrease
Answers:
increase
As we increase \lambda, the model variance of the model \vec{h} = X \vec{w}_\text{ridge}^* tends to ____.
increase
stay the same
decrease
Answers:
decrease
As we increase \lambda, the observation variance of the model \vec{h} = X \vec{w}_\text{ridge}^* tends to ____.
increase
stay the same
decrease
Answers:
stay the same
Neerad wants to build a model that predicts the number of open rooms a hotel has, given various other features. He has a training set with 1200 rows available to him for the purposes of training his model.
Neerad fits a regression model using the GPTRegression
class. GPTRegression models have several hyperparameters
that can be tuned, including context_length and
sentience.
To choose between 5 possible values of the hyperparameter
context_length, Neerad performs k-fold cross-validation.
GPTRegression model fit?4k
5k
240k
6000k
4(k − 1)
5(k − 1)
240(k − 1)
6000(k − 1)
GPTRegression model is fit,
it appends the number of points in its training set to the list
sizes. Note that after performing cross- validation,
len(sizes) is equal to your answer to the previous
subpart.What is sum(sizes)?
4k
5k
240k
6000k
4(k − 1)
5(k − 1)
240(k − 1)
6000(k − 1)
Answers:
When we do k-fold cross-validation for one single hyperparameter value, we split the dataset into k folds, and in each iteration i, train the model on the remaining k-1 folds and evaluate on fold i. Since every fold is left out and evaluated on once, the model is fit in total k times. We do this once for every hyperparameter value we want to test, so the total number of model fits required is 5k.
In part 2, we can note that each model fit is performed on the same size of data – the size of the remaining k-1 folds when we hold out a single fold. This size is 1 - \frac{1}{k} = \frac{k-1}{k} times the size of the entire dataset, in this case, 1200 \cdot \frac{k-1}{k}, and we fit a model on a dataset of this size 5k times. So, the sum of the training sizes for each model fit is:
5k \cdot \frac{k-1}{k} \cdot 1200 = 6000(k-1)
The average training error and validation error for all 5 candidate
values of context_length are given below.
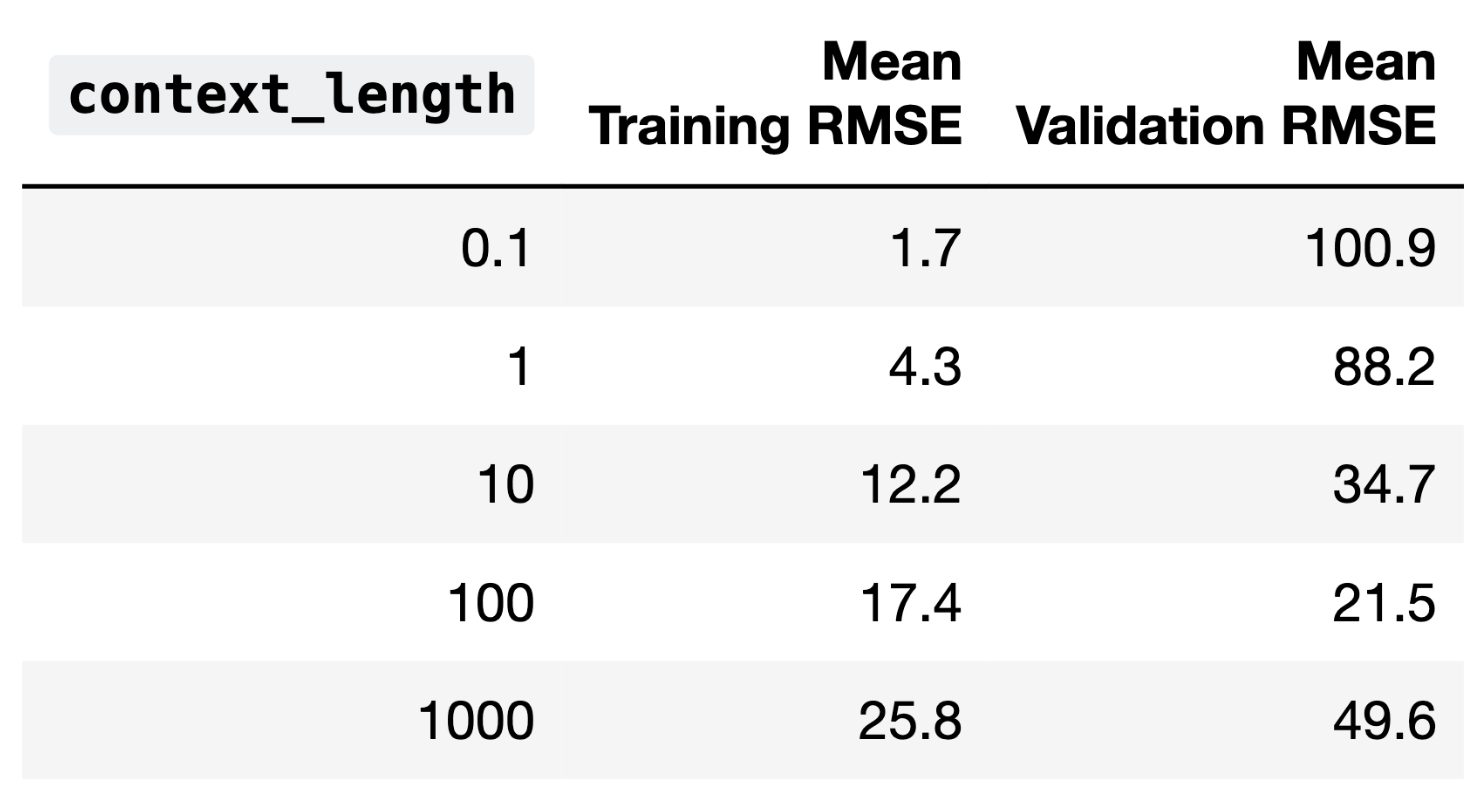
Fill in the blanks: As context_length increases, model
complexity __(i)__. The optimal choice of
context_length is __(ii)__; if we choose a
context_length any higher than that, our model will
__(iii)__.
None
decreases
0.1
1
10
100
1000
overfit the training data and have high bias
underfit the training data and have high bias
overfit the training data and have low bias
underfit the training data and have low bias
Answers:
In part 1, we can see that as context_length increases,
the training error increases, and the model performs worse. In general,
higher model complexity leads to better model performance, so here,
increasing context_length is reducing model
complexity.
In part 2, we will choose a context_length of 100, since
this parameterization leads to the best validation performance. If we
increase context_length further, the validation error
increases.
In part 3, since increased context_length indicates
less complexity and worse training performance, increasing the
context_length further would lead to underfitting, as the
model would lack the expressiveness or number of parameters required to
capture the data. Since training error represents model bias, and since
high variance is associated with overfitting, a further
increase in context_length would mean a more biased
model.
Suppose we want to use logistic regression to classify whether a person survived the sinking of the Titanic. The first 5 rows of our dataset are given below.
\begin{array}{|c|c|c|c|} \hline & \textbf{Age} & \textbf{Survived} & \textbf{Female} \\ \hline 0 & 22.0 & 0 & 0 \\ \hline 1 & 38.0 & 1 & 1 \\ \hline 2 & 26.0 & 1 & 1 \\ \hline 3 & 35.0 & 1 & 1 \\ \hline 4 & 35.0 & 0 & 0 \\ \hline \end{array}
Suppose after training our logistic regression model we get \vec{w}^* = \begin{bmatrix} -1.2 \\ -0.005 \\ 2.5 \end{bmatrix}, where -1.2 is an intercept term, -0.005 is the optimal parameter corresponding to passenger’s age, and 2.5 is the optimal parameter corresponding to sex (1 if female, 0 otherwise).
Consider Sı̄lānah Iskandar Nāsı̄f Abı̄ Dāghir Yazbak, a 20 year old female. What chance did she have to survive the sinking of the Titanic according to our model? Give your answer as a probability in terms of \sigma. If there is not enough information, write “not enough information.”
Answer: P(y_i = 1 | \text{age}_i = 20, \text{female}_i = 1) = \sigma(1.2)
Recall, the logistic regression model predicts the probability of surviving the Titanic as:
P(y_i = 1 | \vec x_i) = \sigma(\vec w^* \cdot \text{Aug}(\vec x_i))
where \sigma(\cdot) represents the logistic function, \sigma(t) = \frac{1}{1 + e^{-t}}.
Here, our augmented feature vector is of the form \text{Aug}(\vec{x}_i) = \begin{bmatrix} 1 \\ 20 \\ 1 \end{bmatrix}. Then \vec{w}^* \cdot \text{Aug}(\vec x_i) = 1(-1.2) + 20(-0.005) + 1(2.5) = 1.2.
Putting this all together, we have:
P(y_i = 1 | \vec{x}_i) = \sigma \left( \vec{w}^* \cdot \text{Aug}(\vec x_i) \right) = \boxed{\sigma (1.2)}
Sı̄lānah Iskandar Nāsı̄f Abı̄ Dāghir Yazbak actually survived. What is the cross-entropy loss for our prediction in the previous part?
Answer: -\log (\sigma (1.2))
Here y_i=1 and p_i = \sigma (1.2). The formula for cross entropy loss is:
L_\text{ce}(y_i, p_i) = -y_i\log (p_i) - (1 - y_i)\log (1 - p_i) = \boxed{-\log (\sigma (1.2))}
At what age would we predict that a female passenger is more likely to have survived the Titanic than not? In other words, at what age is the probability of survival for a female passenger greater than 0.5?
Hint: Since \sigma(0) = 0.5, we have that \sigma \left( \vec{w}^* \cdot \text{Aug}(\vec x_i) \right) = 0.5 \implies \vec{w}^* \cdot \text{Aug}(\vec x_i) = 0.
Answer: 260 years old
The probability that a female passenger of age a survives the Titanic is:
P(y_i = 1 | \text{age}_i = a, \text{female}_i = 1) = \sigma(-1.2 - 0.005 a + 2.5) = \sigma(1.3 - 0.005a)
In order for \sigma(1.3 - 0.005a) = 0.5, we need 1.3 - 0.005a = 0. This means that:
0.005a = 1.3 \implies a = \frac{1.3}{0.005} = 1.3 \cdot 200 = 260
So, a female passenger must be at least 260 years old in order for us to predict that they are more likely to survive the Titanic than not. Note that \text{age} = 260 can be interpreted as a decision boundary; since we’ve fixed a value for the \text{female} feature, there’s only one remaining feature, which is \text{age}. Because the coefficient associated with age is negative, any age larger than 260 causes the probability of surviving to decrease.
Let m be the odds of a given non-female passenger’s survival according to our logistic regression model, i.e., if the passenger had an 80% chance of survival, m would be 4, since their odds of survival are \frac{0.8}{0.2} = 4.
It turns out we can compute f, the odds of survival for a female passenger of the same age, in terms of m. Give an expression for f in terms of m.
Let p_m be the probability that the non-female passenger survives, and let p_f be the probability that the female passenger of the same age survives. Then, we have that:
p_m = \sigma(-1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 0)
p_f = \sigma(-1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 1)
Now, recall from Lecture 22 that:
What does this all have to do with the question? Well, we can take the two equations at the start of the solution and apply \sigma^{-1} to both sides, yielding:
\sigma^{-1}(p_m) = -1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 0
\sigma^{-1}(p_f) = -1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 1
But, \sigma^{-1}(p_m) = \log \left( \text{odds}(p_m) \right) = \log(m) (using the definition in the problem) and \sigma^{-1}(p_f) = \log \left( \text{odds}(p_f) \right) = \log(f), so we have that:
\log(m) = -1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 0
\log(f) = -1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 1
Finally, if we raise both sides to the exponent e, we’ll be able to directly write f in terms of m! Remember that e^{\log(m)} = m and e^{\log(f)} = f, assuming that we’re using the natural logarithm. Then:
m = e^{-1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 0}
f = e^{-1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 1}
So, f in terms of m is:
\frac{f}{m} = \frac{e^{-1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 1}}{e^{-1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 0}} = e^{2.5}
Or, in other words:
\boxed{f = e^{2.5}m}
We decide to build a classifier that takes in a state’s demographic information and predicts whether, in a given year:
The state’s mean math score was greater than its mean verbal score (1), or
the state’s mean math score was less than or equal to its mean verbal score (0).
The simplest possible classifier we could build is one that predicts the same label (1 or 0) every time, independent of all other features.
Consider the following statement:
If a > b, then the constant classifier that
maximizes training accuracy predicts 1 every time; otherwise, it
predicts 0 every time.
For which combination of a and b is the
above statement not guaranteed to be true?
Note: Treat sat as our training set.
Option 1:
a = (sat['Math'] > sat['Verbal']).mean()
b = 0.5Option 2:
a = (sat['Math'] - sat['Verbal']).mean()
b = 0Option 3:
a = (sat['Math'] - sat['Verbal'] > 0).mean()
b = 0.5Option 4:
a = ((sat['Math'] / sat['Verbal']) > 1).mean() - 0.5
b = 0Option 1
Option 2
Option 3
Option 4
Answer: Option 2
Conceptually, we’re looking for a combination of a and
b such that when a > b, it’s true that
in more than 50% of states, the "Math" value is
larger than the "Verbal" value. Let’s look at all
four options through this lens:
sat['Math'] > sat['Verbal'] is a Series of
Boolean values, containing True for all states where the
"Math" value is larger than the "Verbal" value
and False for all other states. The mean of this series,
then, is the proportion of states satisfying this criteria, and since
b is 0.5, a > b is
True only when the bolded condition above is
True.sat['Math'] / sat['Verbal'] is a Series that
contains values greater than 1 whenever a state’s "Math"
value is larger than its "Verbal" value and less than or
equal to 1 in all other cases. As in the other options that work,
(sat['Math'] / sat['Verbal']) > 1 is a Boolean Series
with True for all states with a larger "Math"
value than "Verbal" values; a > b compares
the proportion of True values in this Series to 0.5. (Here,
p - 0.5 > 0 is the same as p > 0.5.)Then, by process of elimination, Option 2 must be the correct option
– that is, it must be the only option that doesn’t
work. But why? sat['Math'] - sat['Verbal'] is a Series
containing the difference between each state’s "Math" and
"Verbal" values, and .mean() computes the mean
of these differences. The issue is that here, we don’t care about
how different each state’s "Math" and
"Verbal" values are; rather, we just care about the
proportion of states with a bigger "Math" value than
"Verbal" value. It could be the case that 90% of states
have a larger "Math" value than "Verbal"
value, but one state has such a big "Verbal" value that it
makes the mean difference between "Math" and
"Verbal" scores negative. (A property you’ll learn about in
future probability courses is that this is equal to the difference in
the mean "Math" value for all states and the mean
"Verbal" value for all states – this is called the
“linearity of expectation” – but you don’t need to know that to answer
this question.)
Suppose we train a classifier, named Classifier 1, and it achieves an accuracy of \frac{5}{9} on our training set.
Typically, root mean squared error (RMSE) is used as a performance metric for regression models, but mathematically, nothing is stopping us from using it as a performance metric for classification models as well.
What is the RMSE of Classifier 1 on our training set? Give your answer as a simplified fraction.
Answer: \frac{2}{3}
An accuracy of \frac{5}{9} means that the model is such that out of 9 values, 5 are labeled correctly. By extension, this means that 4 out of 9 are not labeled correctly as 0 or 1.
Remember, RMSE is defined as
\text{RMSE} = \sqrt{\frac{1}{n} \sum_{i = 1}^n (y_i - H(x_i))^2}
where y_i represents the ith actual value and H(x_i) represents the ith prediction. Here, y_i is either 0 or 1 and $H(x_i) is also either 0 or 1. We’re told that \frac{5}{9} of the time, y_i and H(x_i) are the same; in those cases, (y_i - H(x_i))^2 = 0^2 = 0. We’re also told that \frac{4}{9} of the time, y_i and H(x_i) are different; in those cases, (y_i - H(x_i))^2 = 1. So,
\text{RMSE} = \sqrt{\frac{5}{9} \cdot 0 + \frac{4}{9} \cdot 1} = \sqrt{\frac{4}{9}} = \frac{2}{3}
While Classifier 1’s accuracy on our training set is \frac{5}{9}, its accuracy on our test set is \frac{1}{4}. Which of the following scenarios is most likely?
Classifier 1 overfit to our training set; we need to increase its complexity.
Classifier 1 overfit to our training set; we need to decrease its complexity.
Classifier 1 underfit to our training set; we need to increase its complexity.
Classifier 1 underfit to our training set; we need to decrease its complexity.
Answer: Option 2
Since the accuracy of Classifier 1 is much higher on the dataset used to train it than the dataset it was tested on, it’s likely Classifer 1 overfit to the training set because it was too complex. To fix the issue, we need to decrease its complexity, so that it focuses on learning the general structure of the data in the training set and not too much on the random noise in the training set.
For the remainder of this question, suppose we train another classifier, named Classifier 2, again on our training set. Its performance on the training set is described in the confusion matrix below. Note that the columns of the confusion matrix have been separately normalized so that each has a sum of 1.
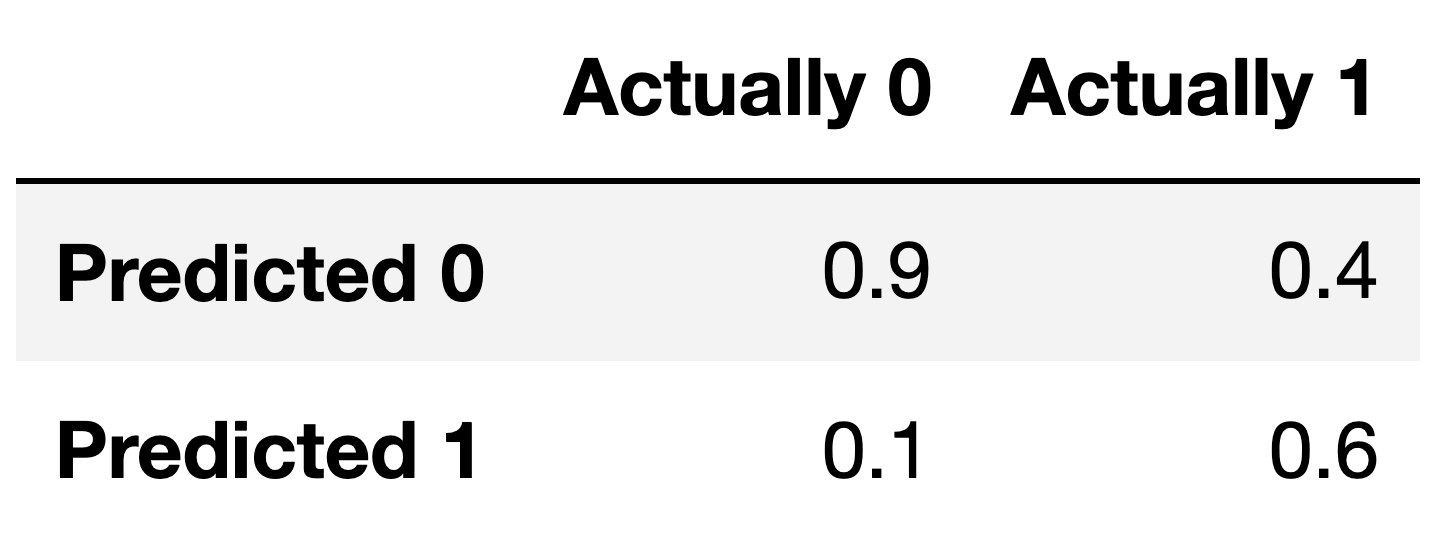
Suppose conf is the DataFrame above. Which of the
following evaluates to a Series of length 2 whose only unique value is
the number 1?
conf.sum(axis=0)
conf.sum(axis=1)
Answer: Option 1
Note that the columns of conf sum to 1 – 0.9 + 0.1 = 1, and 0.4 + 0.6 = 1. To create a Series with just
the value 1, then, we need to sum the columns of conf,
which we can do using conf.sum(axis=0).
conf.sum(axis=1) would sum the rows of
conf.
Fill in the blank: the ___ of Classifier 2 is guaranteed to be 0.6.
precision
recall
Answer: recall
The number 0.6 appears in the bottom-right corner of
conf. Since conf is column-normalized, the
value 0.6 represents the proportion of values in the second column that
were predicted to be 1. The second column contains values that were
actually 1, so 0.6 is really the proportion of values that were
actually 1 that were predicted to be 1, that is, \frac{\text{actually 1 and predicted
1}}{\text{actually 1}}. This is the definition of recall!
If you’d like to think in terms of true positives, etc., then remember that: - True Positives (TP) are values that were actually 1 and were predicted to be 1. - True Negatives (TN) are values that were actually 0 and were predicted to be 0. - False Positives (FP) are values that were actually 0 and were predicted to be 1. - False Negatives (FN) are values that were actually 1 and were predicted to be 0.
Recall is \frac{\text{TP}}{\text{TP} + \text{FN}}.
For your convenience, we show the column-normalized confusion matrix from the previous page below. You will need to use the specific numbers in this matrix when answering the following subpart.

Suppose a fraction \alpha of the labels in the training set are actually 1 and the remaining 1 - \alpha are actually 0. The accuracy of Classifier 2 is 0.65. What is the value of \alpha?
Hint: If you’re unsure on how to proceed, here are some guiding questions:
Suppose the number of y-values that are actually 1 is A and that the number of y-values that are actually 0 is B. In terms of A and B, what is the accuracy of Classifier 2? Remember, you’ll need to refer to the numbers in the confusion matrix above.
What is the relationship between A, B, and \alpha? How does it simplify your calculation for the accuracy in the previous step?
Answer: \frac{5}{6}
Here is one way to solve this problem:
accuracy = \frac{TP + TN}{TP + TN + FP + FN}
Given the values from the confusion matrix:
accuracy = \frac{0.6 \cdot \alpha + 0.9
\cdot (1 - \alpha)}{\alpha + (1 - \alpha)}
accuracy = \frac{0.6 \cdot \alpha + 0.9 - 0.9
\cdot \alpha}{1}
accuracy = 0.9 - 0.3 \cdot \alpha
Therefore:
0.65 = 0.9 - 0.3 \cdot \alpha
0.3 \cdot \alpha = 0.9 - 0.65
0.3 \cdot \alpha = 0.25
\alpha = \frac{0.25}{0.3}
\alpha = \frac{5}{6}
Let \vec{x} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}. Consider the function g(\vec{x}) = (x_1 - 3)^2 + (x_1^2 - x_2)^2.
Find \nabla g(\vec{x}), the gradient of g(\vec{x}), and use it to show that \nabla g\left( \begin{bmatrix} -1 \\ 1 \end{bmatrix} \right) = \begin{bmatrix} -8 \\ 0 \end{bmatrix}.
\nabla g(\vec{x}) = \begin{bmatrix} 2x_1 -6 + 4x_1(x_1^2 - x_2) \\ -2(x_1^2 - x_2) \end{bmatrix}
We can find \nabla g(\vec{x}) by finding the partial derivatives of g(\vec{x}):
\frac{\partial g}{\partial x_1} = 2(x_1 - 3) + 2(x_1^2 - x_2)(2 x_1) \frac{\partial g}{\partial x_2} = 2(x_1^2 - x_2)(-1) \nabla g(\vec{x}) = \begin{bmatrix} 2(x_1 - 3) + 2(x_1^2 - x_2)(2 x_1) \\ 2(x_1^2 - x_2)(-1) \end{bmatrix} \nabla g\left(\begin{bmatrix} - 1 \\ 1 \end{bmatrix}\right) = \begin{bmatrix} 2(-1 - 4) + 2((-1)^2 - 1)(2(-1)) \\ 2((-1)^2 - 1) \end{bmatrix} = \begin{bmatrix} -8 \\ 0 \end{bmatrix}.
We’d like to find the vector \vec{x}^* that minimizes g(\vec{x}) using gradient descent. Perform one iteration of gradient descent by hand, using the initial guess \vec{x}^{(0)} = \begin{bmatrix} -1 \\ 1 \end{bmatrix} and the learning rate \alpha = \frac{1}{2}. In other words, what is \vec{x}^{(1)}?
\vec x^{(1)} = \begin{bmatrix} 3 \\ 1 \end{bmatrix}
Here’s the general form of gradient descent: \vec x^{(1)} = \vec{x}^{(0)} - \alpha \nabla g(\vec{x}^{(0)})
We can substitute \alpha = \frac{1}{2} and x^{(0)} = \begin{bmatrix} -1 \\ 1 \end{bmatrix} to get: \vec x^{(1)} = \begin{bmatrix} -1 \\ 1 \end{bmatrix} - \frac{1}{2} \nabla g(\vec x ^{(0)}) \vec x^{(1)} = \begin{bmatrix} -1 \\ 1 \end{bmatrix} - \frac{1}{2} \begin{bmatrix} -8 \\ 0 \end{bmatrix}
\vec{x}^{(1)} = \begin{bmatrix} -1 \\ 1 \end{bmatrix} - \frac{1}{2} \begin{bmatrix} -8 \\ 0 \end{bmatrix} = \begin{bmatrix} 3 \\ 1 \end{bmatrix}
Consider the function f(t) = (t - 3)^2 + (t^2 - 1)^2. Select the true statement below.
f(t) is convex and has a global minimum.
f(t) is not convex, but has a global minimum.
f(t) is convex, but doesn’t have a global minimum.
f(t) is not convex and doesn’t have a global minimum.
f(t) is not convex, but has a global minimum.
It is seen that f(t) isn’t convex, which can be verified using the second derivative test: f'(t) = 2(t - 3) + 2(t^2 - 1) 2t = 2t - 6 + 4t^3 - 4t = 4t^3 - 2t - 6 f''(t) = 12t^2 - 2
Clearly, f''(t) < 0 for many values of t (e.g. t = 0), so f(t) is not always convex.
However, f(t) does have a global minimum – its output is never less than 0. This is because it can be expressed as the sum of two squares, (t - 3)^2 and (t^2 - 1)^2, respectively, both of which are greater than or equal to 0.