
← return to study.practicaldsc.org
The problems in this worksheet are taken from past exams in similar classes. Work on them on paper, since the exams you take in this course will also be on paper.
Consider the dataset shown below.
| x^{(1)} | x^{(2)} | x^{(3)} | y |
|---|---|---|---|
| 0 | 6 | 8 | -5 |
| 3 | 4 | 5 | 7 |
| 5 | -1 | -3 | 4 |
| 0 | 2 | 1 | 2 |
We want to use multiple regression to fit a prediction rule of the form H(x_i^{(1)}, x_i^{(2)}, x_i^{(3)}) = w_0 + w_1 x_i^{(1)} x_i^{(3)} + w_2 (x_i^{(2)} - x_i^{(3)})^2. Write down the design matrix X and observation vector \vec{y} for this scenario. No justification needed.
The design matrix X and observation vector \vec{y} are given by:
X = \begin{bmatrix} 1 & 0 & 4\\ 1 & 15 & 1\\ 1 & -15 & 4\\ 1 & 0 & 1 \end{bmatrix}
\vec{y} = \begin{bmatrix} -5\\ 7\\ 4\\ 2 \end{bmatrix}
The observation vector \vec{y} contains the target values from the dataset.
For the design matrix X, each row corresponds to one data point in our dataset, where x_i^{(1)}, x_i^{(2)}, and x_i^{(3)} represent three separate features for the i-th data point. Each row of X has the form \begin{bmatrix}1 & x_i^{(1)}x_i^{(3)} & (x_i^{(2)}-x_i^{(3)})^2\end{bmatrix}. The first column consists of all 1’s for the bias term w_0, which is not affected by the feature values.
For the X and \vec{y} that you have written down, let \vec{w} be the optimal parameter vector, which comes from solving the normal equations X^TX\vec{w}=X^T\vec{y}. Let \vec{e} = \vec{y} - X \vec{w} be the error vector, and let e_i be the ith component of this error vector. Show that 4e_1+e_2+4e_3+e_4=0.
The key to this problem is the fact that the error vector, \vec{e}, is orthogonal to the columns of the design matrix, X. As a refresher, if \vec{w^*} satisfies the normal equations, then:
We can rewrite the normal equation (X^TX\vec{w}=X^T\vec{y}) to allow substitution for \vec{e} = \vec{y} - X \vec{w}.
X^TX\vec{w}=X^T\vec{y} 0 = X^T\vec{y} - X^TX\vec{w} 0 = X^T(\vec{y}-X\vec{w}) 0 = X^T\vec{e}
The first step is to find X^T, which is easy because we found X above: \begin{bmatrix} 1 & 1 & 1 & 1 \\ 0 & 15 & -15 & 0 \\ 4 & 1 & 4 & 1 \end{bmatrix}
And now we can plug X^T and \vec e into our equation 0 = X^T\vec{e}. It might be easiest to find the right side first:
X^T\vec{e} = \begin{bmatrix} 1 & 1 & 1 & 1 \\ 0 & 15 & -15 & 0 \\ 4 & 1 & 4 & 1 \end{bmatrix} \cdot \begin{bmatrix} e_1 \\ e_2 \\ e_3 \\ e_4\end{bmatrix}
= \begin{bmatrix} e_1 + e_2 + e_3 + e_4 \\ 15e_2 - 15e_3 \\ 4e_1 + e_2 + 4e_3 + e_4\end{bmatrix}
Finally, we set it equal to zero! 0 = e_1 + e_2 + e_3 + e_4 0 = 15e_2 - 15e_3 0 = 4e_1 + e_2 + 4e_3 + e_4
With this we have shown that 4e_1+e_2+4e_3+e_4=0.
The two plots below show the total number of boots (top) and sandals
(bottom) purchased per month in the df table. Assume that
there is one data point per month.

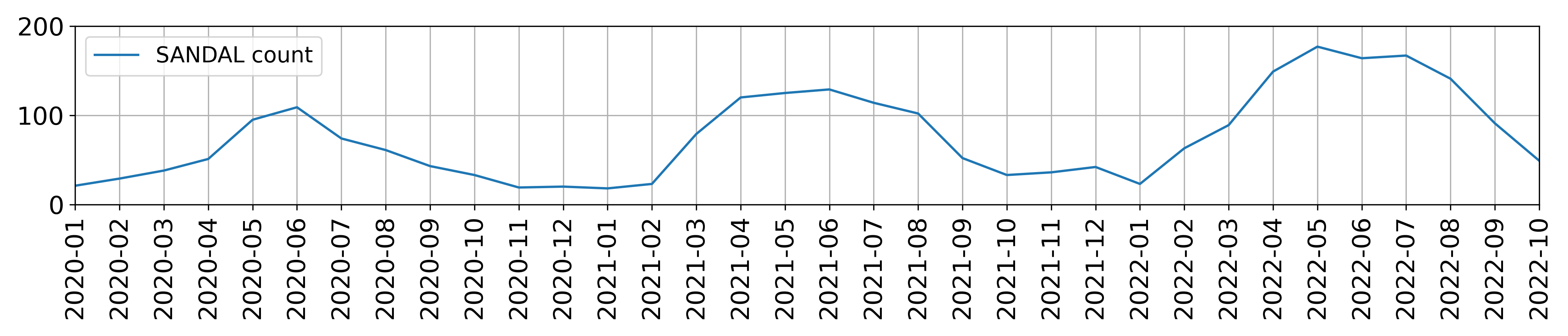
For each of the following regression models, use the visualizations shown above to select the value that is closest to the fitted model weights. If it is not possible to determine the model weight, select “Not enough info”. For the models below:
\text{predicted boot}_i = w_0
w_0:
0
50
100
Not enough info
Answer: w_0 = 50
The model predicts a constant value for boots. The intercept w_0 represents the average boots sold across all months. Since the boot count plot shows data points centered around 50, this is the best estimate.
\text{predicted boot}_i = w_0 + w_1 \cdot \text{sandals}_i
w_0:
-100
-1
0
1
100
Not enough info
w_1:
-100
-1
1
100
Not enough info
Answer:
w_0: 100
The intercept w_0 represents the predicted boot sales when sandal sales are zero. Since the boot plot shows a baseline of ~100 units during months with minimal sandal sales (e.g., winter), this justifies w_0 = 100
w_1: -1
The coefficient w_1 = −1 indicates an inverse relationship: for every additional sandal sold, boot sales decrease by 1 unit. This aligns with seasonal trends (e.g., sandals dominate in summer, boots in winter), and the plots show a consistent negative slope of -1 between the variables.
\text{predicted boot}_i = w_0 + w_1 \cdot (\text{summer=1})_i
w_0:
-100
-1
0
1
100
Not enough info
w_1:
-80
-1
0
1
80
Not enough info
Answer:
w_0: 100
The intercept represents the average boot sales when \text{summer}=0 (winter months). Since the boot plot shows consistent sales of ~100 units during winter, this value is justified.
w_1: -80
The coefficient for \text{summer}=1 reflects the change in boot sales during summer. If boot sales drop sharply by ~80 units in summer (e.g., from 100 in winter to 20 in the summer), this negative offset matches the seasonal trend.
\text{predicted sandal}_i = w_0 + w_1 \cdot (\text{summer=1})_i
w_0:
-20
-1
0
1
20
Not enough info
w_1:
-80
-1
0
1
80
Not enough info
Answer:
w_0: 20
The intercept represents baseline sandal sales when \text{summer}=0 (winter months). Since the sandal plot shows consistent sales of ~20 units during winter, this value aligns with the seasonal low.
w_1: 80
The coefficient reflects the increase in sandal sales during summer. If sales rise sharply by ~80 units in summer (e.g., from 20 in winter to 100 in summer), this positive seasonal effect matches the trend shown in the visualization.
\text{predicted sandal}_i = w_0 + w_1 \cdot (\text{summer=1})_i + w_2 \cdot (\text{winter=1})_i
w_0:
-20
-1
0
1
20
Not enough info
w_1:
-80
-1
0
1
80
Not enough info
w_2:
-80
-1
0
1
80
Not enough info
Answer:
w_0: Not enough info
w_1: Not enough info
w_2: Not enough info
The model includes both () and () variables, which cover all months. This creates multicollinearity. The intercept and coefficients cannot be uniquely determined without a reference category or additional constraints. For example, increasing the intercept and decreasing both seasonal coefficients equally would yield the same predictions. The visualizations do not provide enough information to resolve this ambiguity.
We will aim to build a classifier that takes in demographic information about a state from a particular year and predicts whether or not the state’s mean math score is higher than its mean verbal score that year.
In honor of the
rotisserie
chicken event on UCSD’s campus in March of 2023,
sklearn released a new classifier class called
ChickenClassifier.
ChickenClassifiers have many hyperparameters, one of
which is height. As we increase the value of
height, the model variance of the resulting
ChickenClassifier also increases.
First, we consider the training and testing accuracy of a
ChickenClassifier trained using various values of
height. Consider the plot below.

Which of the following depicts training accuracy
vs. height?
Option 1
Option 2
Option 3
Which of the following depicts testing accuracy
vs. height?
Option 1
Option 2
Option 3
Answer: Option 2 depicts training accuracy
vs. height; Option 3 depicts testing accuract
vs. height
We are told that as height increases, the model variance
(complexity) also increases.
As we increase the complexity of our classifier, it will do a better
job of fitting to the training set because it’s able to “memorize” the
patterns in the training set. As such, as height increases,
training accuracy increases, which we see in Option 2.
However, after a certain point, increasing height will
make our classifier overfit too closely to our training set and not
general enough to match the patterns in other similar datasets, meaning
that after a certain point, increasing height will actually
decrease our classifier’s accuracy on our testing set. The only option
that shows accuracy increase and then decrease is Option 3.
ChickenClassifiers have another hyperparameter,
color, for which there are four possible values:
"yellow", "brown", "red", and
"orange". To find the optimal value of color,
we perform k-fold cross-validation with
k=4. The results are given in the table
below.

Which value of color has the best average validation
accuracy?
"yellow"
"brown"
"red"
"orange"
Answer: "red"
From looking at the results of the k-fold cross validation, we see that the color red has the highest, and therefore the best, validation accuracy as it has the highest row mean (across all 4 folds).
True or False: It is possible for a hyperparameter value to have the best average validation accuracy across all folds, but not have the best validation accuracy in any one particular fold.
True
False
Answer: True
An example is shown below:
| color | Fold 1 | Fold 2 | Fold 3 | Fold 4 | average |
|---|---|---|---|---|---|
| color 1 | 0.8 | 0 | 0 | 0 | 0.2 |
| color 2 | 0 | 0.6 | 0 | 0 | 0.15 |
| color 3 | 0 | 0 | 0.1 | 0 | 0.025 |
| color 4 | 0 | 0 | 0 | 0.2 | 0.05 |
| color 5 | 0.7 | 0.5 | 0.01 | 0.1 | 0.3275 |
In the example, color 5 has the highest average validation accuracy across all folds, but is not the best in any one fold.
Now, instead of finding the best height and best
color individually, we decide to perform a grid search that
uses k-fold cross-validation to find
the combination of height and color with the
best average validation accuracy.
For the purposes of this question, assume that:
height and h_2 possible
values of color.Consider the following three subparts:
Choose from the following options.
k
\frac{k}{n}
\frac{n}{k}
\frac{n}{k} \cdot (k - 1)
h_1h_2k
h_1h_2(k-1)
\frac{nh_1h_2}{k}
None of the above
Answer: A: Option 3 (\frac{n}{k}), B: Option 6 (h_1h_2(k-1)), C: Option 8 (None of the above)
The training set is divided into k folds of equal size, resulting in k folds with size \frac{n}{k}.
For each combination of hyperparameters, row 5 is k - 1 times for training and 1 time for validation. There are h_1 \cdot h_2 combinations of hyperparameters, so row 5 is used for training h_1 \cdot h_2 \cdot (k-1) times.
Building off of the explanation for the previous subpart, row 5 is used for validation 1 times for each combination of hyperparameters, so the correct expression would be h_1 \cdot h_2, which is not a provided option.
Consider the least squares regression model, \vec{h} = X \vec{w}. Assume that X and \vec{h} refer to the design matrix and hypothesis vector for our training data, and \vec y is the true observation vector.
Let \vec{w}_\text{OLS}^* be the parameter vector that minimizes mean squared error without regularization. Specifically:
\vec{w}_\text{OLS}^* = \arg\underset{\vec{w}}{\min} \frac{1}{n} \| \vec{y} - X \vec{w} \|^2_2
Let \vec{w}_\text{ridge}^* be the parameter vector that minimizes mean squared error with L_2 regularization, using a non-negative regularization hyperparameter \lambda (i.e. ridge regression). Specifically:
\vec{w}_\text{ridge}^* = \arg\underset{\vec{w}}{\min} \frac{1}{n} \| \vec y - X \vec{w} \|^2_2 + \lambda \sum_{j=1}^{p} w_j^2
For each of the following problems, fill in the blank.
If we set \lambda = 0, then \Vert \vec{w}_\text{OLS}^* \Vert^2_2 is ____ \Vert \vec{w}_\text{ridge}^* \Vert^2_2
less than
equal to
greater than
impossible to tell
Answers:
equal to
For each of the remaining parts, you can assume that \lambda is set such that the predicted response vectors for our two models (\vec{h} = X \vec{w}_\text{OLS}^* and \vec{h} = X \vec{w}_\text{ridge}^*) is different.
The training MSE of the model \vec{h} = X \vec{w}_\text{OLS}^* is ____ than the model \vec{h} = X \vec{w}_\text{ridge}^*.
less than
equal to
greater than
impossible to tell
Answers:
less than
Now, assume we’ve fit both models using our training data, and evaluate both models on some unseen testing data.
The test MSE of the model \vec{h} = X \vec{w}_\text{OLS}^* is ____ than the model \vec{h} = X \vec{w}_\text{ridge}^*.
less than
equal to
greater than
impossible to tell
Answers:
impossible to tell
Assume that our design matrix X contains a column of all ones. The sum of the residuals of our model \vec{h} = X \vec{w}_\text{ridge}^* ____.
equal to 0
not necessarily equal to 0
Answers:
not necessarily equal to 0
As we increase \lambda, the bias of the model \vec{h} = X \vec{w}_\text{ridge}^* tends to ____.
increase
stay the same
decrease
Answers:
increase
As we increase \lambda, the model variance of the model \vec{h} = X \vec{w}_\text{ridge}^* tends to ____.
increase
stay the same
decrease
Answers:
decrease
As we increase \lambda, the observation variance of the model \vec{h} = X \vec{w}_\text{ridge}^* tends to ____.
increase
stay the same
decrease
Answers:
stay the same
Suppose we’d like to use gradient descent to minimize the function f(x) = x^3 + x^2. Suppose we choose a learning rate of \alpha = \frac{1}{4}.
Suppose x^{(t)} is our guess of the minimizing input x^{*} at timestep t, i.e. x^{(t)} is the result of performing t iterations of gradient descent, given some initial guess. Write an expression for x^{(t+1)}. Your answer should be an expression involving x^{(t)} and some constants.
In general, the update rule for gradient descent is: x^{(t+1)} = x^{(t)} - \alpha \nabla f(x^{(t)}) = x^{(t)} - \alpha \frac{df}{dx}(x^{(t)}), where \alpha is the learning rate or step size. We know that the derivative of f is as follows: \frac{df}{dx} = f'(x) = 3x^2 + 2x, thus the update rule can be written down as: x^{(t+1)} = x^{(t)} - \alpha(3x^{(t)^2} + 2x^{(t)}) = -\frac{3}{4}x^{(t)^2} + \frac{1}{2}x^{(t)}.
Suppose x^{(0)} = -1.
What is the value of x^{(1)}?
Will gradient descent eventually converge, given the initial guess x^{(0)} = -1 and step size \alpha = \frac{1}{4}?
We have f'(x^{(0)}) = f'(-1) = 3(-1)^2 + 2(-1) = 1 > 0, so we go left, and x^{(1)} = x^{(0)} - \alpha f'(x^{(0)}) = -1 - \frac{1}{4} = -\frac{5}{4}. Intuitively, the gradient descent cannot converge in this case because \text{lim}_{x \rightarrow -\infty} f(x) = -\infty,
We need to find all local minimums and local maximums. First, we solve the equation f'(x) = 0 to find all critical points.
We have: f'(x) = 0 \Leftrightarrow 3x^2 + 2x = 0 \Leftrightarrow x = -\frac{2}{3} \ \ \text{and} \ \ x = 0.
Now, we consider the second-order derivative: f''(x) = \frac{d^2f}{dx^2} = 6x + 2.
We have f''(x) = 0 only when x = -1/3. Thus, for x < -1/3, f''(x) is negative or the slope f'(x) decreases; and for x > -1/3, f''(x) is positive or the slope f'(x) increases. Keep in mind that -1 < -2/3 < -1/3 < 0 < 1.
Therefore, f has a local maximum at x = -2/3 and a local minimum at x = 0. If the gradient descent starts at x^{(0)} = -1 and it always goes left then it will never meet the local minimum at x = 0, and it will go left infinitely. We say the gradient descent cannot converge, or is divergent.
Suppose x^{(0)} = 1.
What is the value of x^{(1)}?
Will gradient descent eventually converge, given the initial guess x^{(0)} = 1 and step size \alpha = \frac{1}{4}?
We have f'(x^{(0)}) = f'(-1) = 3 \cdot 1^2 + 2 \cdot 1 = 5 > 0, so we go left, and x^{(1)} = x^{(0)} - \alpha f'(x^{(0)}) = 1 - \frac{1}{4} \cdot 5 = -\frac{1}{4}.
From the previous part, function f has a local minimum at x = 0, so the gradient descent can converge (given appropriate step size) at this local minimum.
For a given classifier, suppose the first 10 predictions of our classifier and 10 true observations are as follows: \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline \textbf{Predictions} & 1 & 1 & 1 & 1 & 1 & 0 & 1 & 1 & 1 & 1 \\ \hline \textbf{True Label} & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ \hline \end{array}
What is the accuracy of our classifier on these 10 predictions?
What is the precision on these 10 predictions?
What is the recall on these 10 predictions?
Answer:
Let’s first identify all elements of the confusion matrix by comparing predictions with true labels:
| Metric | Count | Explanation |
|---|---|---|
| True Positives (TP) | 6 | Prediction=1 and True Label=1 |
| False Positives (FP) | 3 | Prediction=1 and True Label=0 |
| True Negatives (TN) | 1 | Prediction=0 and True Label=0 |
| False Negatives (FN) | 0 | Prediction=0 and True Label=1 |
| Total | 10 | Total number of predictions |
Accuracy: The proportion of correct predictions (TP + TN) among the total number of predictions. \text{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN} = \frac{6 + 1}{10} = \frac{7}{10} = 0.7
Precision: The proportion of true positives among all positive predictions. \text{Precision} = \frac{TP}{TP + FP} = \frac{6}{6 + 3} = \frac{6}{9} = \frac{2}{3} \approx 0.67
Recall: The proportion of true positives among all actual positives. \text{Recall} = \frac{TP}{TP + FN} = \frac{6}{6 + 0} = \frac{6}{6} = 1
Suppose we want to use logistic regression to classify whether a person survived the sinking of the Titanic. The first 5 rows of our dataset are given below.
\begin{array}{|c|c|c|c|} \hline & \textbf{Age} & \textbf{Survived} & \textbf{Female} \\ \hline 0 & 22.0 & 0 & 0 \\ \hline 1 & 38.0 & 1 & 1 \\ \hline 2 & 26.0 & 1 & 1 \\ \hline 3 & 35.0 & 1 & 1 \\ \hline 4 & 35.0 & 0 & 0 \\ \hline \end{array}
Suppose after training our logistic regression model we get \vec{w}^* = \begin{bmatrix} -1.2 \\ -0.005 \\ 2.5 \end{bmatrix}, where -1.2 is an intercept term, -0.005 is the optimal parameter corresponding to passenger’s age, and 2.5 is the optimal parameter corresponding to sex (1 if female, 0 otherwise).
Consider Sı̄lānah Iskandar Nāsı̄f Abı̄ Dāghir Yazbak, a 20 year old female. What chance did she have to survive the sinking of the Titanic according to our model? Give your answer as a probability in terms of \sigma. If there is not enough information, write “not enough information.”
Answer: P(y_i = 1 | \text{age}_i = 20, \text{female}_i = 1) = \sigma(1.2)
Recall, the logistic regression model predicts the probability of surviving the Titanic as:
P(y_i = 1 | \vec x_i) = \sigma(\vec w^* \cdot \text{Aug}(\vec x_i))
where \sigma(\cdot) represents the logistic function, \sigma(t) = \frac{1}{1 + e^{-t}}.
Here, our augmented feature vector is of the form \text{Aug}(\vec{x}_i) = \begin{bmatrix} 1 \\ 20 \\ 1 \end{bmatrix}. Then \vec{w}^* \cdot \text{Aug}(\vec x_i) = 1(-1.2) + 20(-0.005) + 1(2.5) = 1.2.
Putting this all together, we have:
P(y_i = 1 | \vec{x}_i) = \sigma \left( \vec{w}^* \cdot \text{Aug}(\vec x_i) \right) = \boxed{\sigma (1.2)}
Sı̄lānah Iskandar Nāsı̄f Abı̄ Dāghir Yazbak actually survived. What is the cross-entropy loss for our prediction in the previous part?
Answer: -\log (\sigma (1.2))
Here y_i=1 and p_i = \sigma (1.2). The formula for cross entropy loss is:
L_\text{ce}(y_i, p_i) = -y_i\log (p_i) - (1 - y_i)\log (1 - p_i) = \boxed{-\log (\sigma (1.2))}
At what age would we predict that a female passenger is more likely to have survived the Titanic than not? In other words, at what age is the probability of survival for a female passenger greater than 0.5?
Hint: Since \sigma(0) = 0.5, we have that \sigma \left( \vec{w}^* \cdot \text{Aug}(\vec x_i) \right) = 0.5 \implies \vec{w}^* \cdot \text{Aug}(\vec x_i) = 0.
Answer: 260 years old
The probability that a female passenger of age a survives the Titanic is:
P(y_i = 1 | \text{age}_i = a, \text{female}_i = 1) = \sigma(-1.2 - 0.005 a + 2.5) = \sigma(1.3 - 0.005a)
In order for \sigma(1.3 - 0.005a) = 0.5, we need 1.3 - 0.005a = 0. This means that:
0.005a = 1.3 \implies a = \frac{1.3}{0.005} = 1.3 \cdot 200 = 260
So, a female passenger must be at least 260 years old in order for us to predict that they are more likely to survive the Titanic than not. Note that \text{age} = 260 can be interpreted as a decision boundary; since we’ve fixed a value for the \text{female} feature, there’s only one remaining feature, which is \text{age}. Because the coefficient associated with age is negative, any age larger than 260 causes the probability of surviving to decrease.
Let m be the odds of a given non-female passenger’s survival according to our logistic regression model, i.e., if the passenger had an 80% chance of survival, m would be 4, since their odds of survival are \frac{0.8}{0.2} = 4.
It turns out we can compute f, the odds of survival for a female passenger of the same age, in terms of m. Give an expression for f in terms of m.
Let p_m be the probability that the non-female passenger survives, and let p_f be the probability that the female passenger of the same age survives. Then, we have that:
p_m = \sigma(-1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 0)
p_f = \sigma(-1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 1)
Now, recall from Lecture 22 that:
What does this all have to do with the question? Well, we can take the two equations at the start of the solution and apply \sigma^{-1} to both sides, yielding:
\sigma^{-1}(p_m) = -1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 0
\sigma^{-1}(p_f) = -1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 1
But, \sigma^{-1}(p_m) = \log \left( \text{odds}(p_m) \right) = \log(m) (using the definition in the problem) and \sigma^{-1}(p_f) = \log \left( \text{odds}(p_f) \right) = \log(f), so we have that:
\log(m) = -1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 0
\log(f) = -1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 1
Finally, if we raise both sides to the exponent e, we’ll be able to directly write f in terms of m! Remember that e^{\log(m)} = m and e^{\log(f)} = f, assuming that we’re using the natural logarithm. Then:
m = e^{-1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 0}
f = e^{-1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 1}
So, f in terms of m is:
\frac{f}{m} = \frac{e^{-1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 1}}{e^{-1.2 - 0.005 \cdot \text{age} + 2.5 \cdot 0}} = e^{2.5}
Or, in other words:
\boxed{f = e^{2.5}m}
Consider the following dataset of n=7 points in d=2 dimensions.
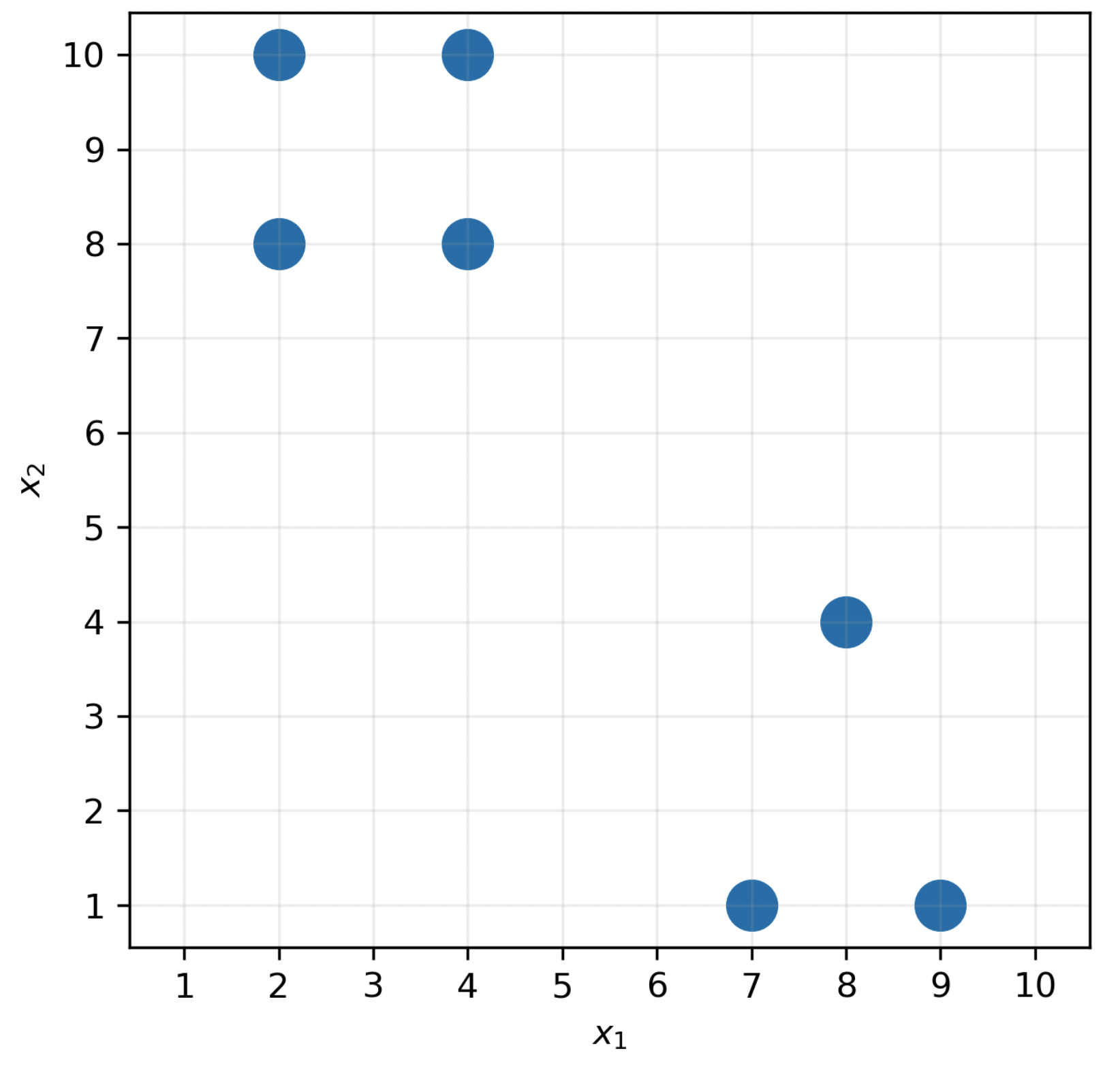
Suppose we decide to use agglomerative clustering to cluster the data. How many possible pairs of clusters could we combine in the first iteration?
Answer: 5
Recall, in agglomerative clustering, we combine the two closest clusters at each iteration. In the first iteration, each point is in its own cluster. There are 5 pairs of points that are all at a distance of 2 units from each other, and no pair of points is closer than 2 units.
Specifically, any two adjacent vertices in the “square” in the top left are 2 units apart (top left and top right, top right and bottom right, bottom left and bottom right, bottom left and top left), which adds to 4 pairs. Then, the bottom two vertices in the triangle in the bottom left are also 2 units apart. This totals 4 + 1 = 5 pairs of points that are all at a distance of 2 units from each other, so there are 5 possible clusters we could combine in the first iteration.
Suppose we want to identify k=2 clusters in this dataset using k-means clustering.
Determine the centroids \vec{\mu}_1 and \vec{\mu}_2 that minimize inertia. (Let \vec{\mu}_1 be the centroid with a smaller x_1 coordinate.) Justify your answers.
Note: You don’t have to run the k-Means Clustering algorithm to answer this question.
Answer: \vec{\mu}_1 = \begin{bmatrix} 3 \\ 9 \end{bmatrix}, \vec{\mu}_2 = \begin{bmatrix} 8 \\ 2 \end{bmatrix}
It’s clear that there are two clusters — one in the top left, and one in the bottom right.
To find \vec{\mu}_1, the centroid for the top-left cluster, we take the mean of four points assigned to cluster 1, giving
\vec{\mu}_1 = \frac{1}{4} \left( \begin{bmatrix} 2 \\ 8 \end{bmatrix} + \begin{bmatrix} 4 \\ 8 \end{bmatrix} + \begin{bmatrix} 2 \\ 10 \end{bmatrix} + \begin{bmatrix} 4 \\ 10 \end{bmatrix} \right) = \begin{bmatrix} 3 \\ 9 \end{bmatrix}
You can also arrive at this result without any algebra by taking the middle of the ‘square’.
To find \vec{\mu}_2, the centroid for the bottom-right cluster, we take the mean of three points assigned to cluster 2, giving
\vec{\mu}_2 = \frac{1}{3} \left( \begin{bmatrix} 7 \\ 1 \end{bmatrix} + \begin{bmatrix} 8 \\ 4 \end{bmatrix} + \begin{bmatrix} 9 \\ 1 \end{bmatrix} \right) = \begin{bmatrix} 8 \\ 2 \end{bmatrix}
Thus,
\vec{\mu}_1 = \begin{bmatrix} 3 \\ 9 \end{bmatrix}, \vec{\mu}_2 = \begin{bmatrix} 8 \\ 2 \end{bmatrix}
What is the total inertia for the centroids you chose in the previous part? Show your work.
Answer: 16
We’ll proceed by determining the inertia of each cluster individually and adding the results together.
First, let’s consider the top-left cluster, whose centroid is at \begin{bmatrix} 3 \\ 9 \end{bmatrix}. The squared distance between the centroid and each of the four points in the cluster individually is 1^2 + 1^2 = 2. It’s easiest to see this by drawing a picture, but we can calculate all squared distances algebraically as well:
\begin{bmatrix} 2 \\ 8 \end{bmatrix} - \begin{bmatrix} 3 \\ 9 \end{bmatrix} = \begin{bmatrix} -1 \\ -1 \end{bmatrix} \implies \text{squared distance} = (-1)^2 + (-1)^2 = 2
\begin{bmatrix} 4 \\ 8 \end{bmatrix} - \begin{bmatrix} 3 \\ 9 \end{bmatrix} = \begin{bmatrix} 1 \\ -1 \end{bmatrix} \implies \text{squared distance} = (1)^2 + (-1)^2 = 2
\begin{bmatrix} 2 \\ 10 \end{bmatrix} - \begin{bmatrix} 3 \\ 9 \end{bmatrix} = \begin{bmatrix} -1 \\ 1 \end{bmatrix} \implies \text{squared distance} = (-1)^2 + (1)^2 = 2
\begin{bmatrix} 4 \\ 10 \end{bmatrix} - \begin{bmatrix} 3 \\ 9 \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \implies \text{squared distance} = (1)^2 + (1)^2 = 2
Thus, the inertia for cluster 1 is 2 + 2 + 2 + 2 = 8.
We follow a similar procedure for cluster 2:
\begin{bmatrix} 7 \\ 1 \end{bmatrix} - \begin{bmatrix} 8 \\ 2 \end{bmatrix} = \begin{bmatrix} -1 \\ -1 \end{bmatrix} \implies \text{squared distance} = (-1)^2 + (-1)^2 = 2
\begin{bmatrix} 8 \\ 4 \end{bmatrix} - \begin{bmatrix} 8 \\ 2 \end{bmatrix} = \begin{bmatrix} 0 \\ 2 \end{bmatrix} \implies \text{squared distance} = (0)^2 + (2)^2 = 4
\begin{bmatrix} 9 \\ 1 \end{bmatrix} - \begin{bmatrix} 8 \\ 2 \end{bmatrix} = \begin{bmatrix} 1 \\ -1 \end{bmatrix} \implies \text{squared distance} = (-1)^2 + (1)^2 = 2
Thus, the inertia for cluster 2 is 2 + 4 + 2 = 8.
This means that the total inertia for the whole dataset is 8 + 8 = 16.