← return to study.practicaldsc.org
The problems in this worksheet are taken from past exams in similar classes. Work on them on paper, since the exams you take in this course will also be on paper.
Consider the following assignment statement.
puffin = np.array([5, 9, 13, 17, 21])Provide arguments to call np.arange with so that the
array penguin is identical to the array
puffin.
penguin = np.arange(____)Answer: We need to provide np.arange
with three arguments: 5, anything in (21,
25], 4. For instance, something line
penguin = np.arange(5, 25, 4) would work.
Fill in the blanks so that the array parrot is also
identical to the array puffin.
Hint: Start by choosing y so that
parrot has length 5.
parrot = __(x)__ * np.arange(0, __(y)__, 2) + __(z)__Answer:
x: 2y: anything in (8,
10]z: 5Suppose we run the following code to simulate the winners of the Tour de France.
evenepoel_wins = 0
vingegaard_wins = 0
pogacar_wins = 0
for i in np.arange(4):
result = np.random.multinomial(1, [0.3, 0.3, 0.4])
if result[0] == 1:
evenepoel_wins = evenepoel_wins + 1
elif result[1] == 1:
vingegaard_wins = vingegaard_wins + 1
elif result[2] == 1:
pogacar_wins = pogacar_wins + 1What is the probability that pogacar_wins is equal to 4
when the code finishes running? Do not simplify your answer.
Answer: 0.4 ^ 4
np.random.multinomial(1, [0.3, 0.3, 0.4]).pogacar wins in a single iteration
is 0.4 (the third entry in the probability vector
[0.3, 0.3, 0.4]).pogacar must win
independently in each iteration.What is the probability that evenepoel_wins is at least
1 when the code finishes running? Do not simplify your answer.
Answer: 1 - 0.7 ^ 4
evenepoel wins in a single
iteration is 0.3 (the first entry in the probability vector
[0.3, 0.3, 0.4]).evenepoel does not
win in a single iteration is: 1 - 0.3 = 0.7evenepoel to win no iterations across all 4 loops,
they must fail to win independently in each iteration:
0.7 * 0.7 * 0.7 * 0.7 = 0.7 ^
4evenepoel_wins is at least 1 is
then: 1 - 0.7 ^ 4After getting bored flipping coins, Caleb decides to use the new skills he learned from lecture to create a simulation.
He defines the 2-D array A as follows:
# .flatten() reshapes from 50 x 2 to 1 x 100
A = np.array([
np.array([np.random.permutation([0, 1]) for _ in range(50)]).flatten()
for _ in range(3000)
])He also defines the 2-D array B as follows:
# .flatten() reshapes from 50 x 2 to 1 x 100
B = np.array([
np.array([np.random.choice([0, 1], 2) for _ in range(50)]).flatten()
for _ in range(3000)
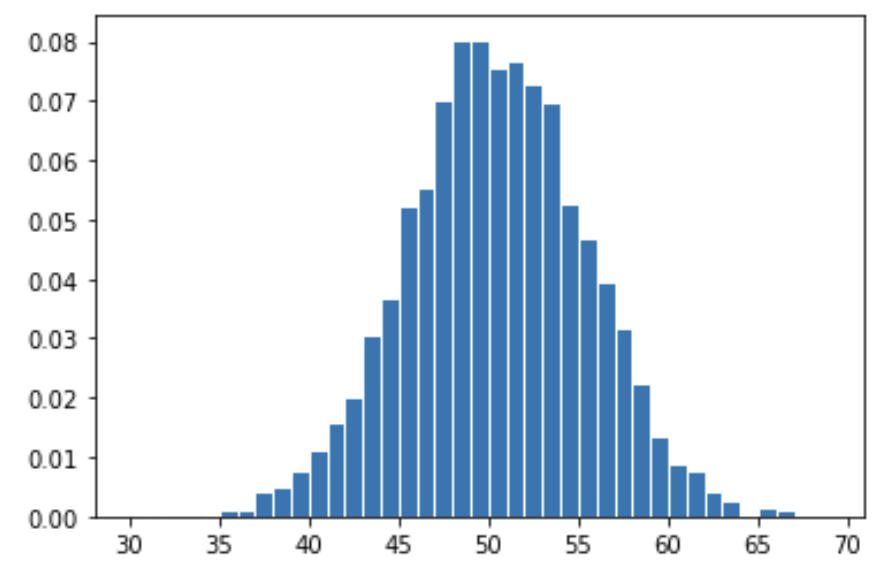
])Below, we see a histogram of the distribution resulting from this simulation.

Which one of the following arrays are visualized above?
A.sum(axis=1)
B.sum(axis=1)
Answer: Option 2
Note that arr.sum(axis=1) takes the sum of each
row of arr.
The difference comes down to the behavior of
np.random.permutation([0, 1]) and
np.random.choice([0, 1]).
Each call to np.random.permutation([0, 1]) will either
return array([0, 1]) or array([1, 0]) — one
head and one tail. As a result, each row of A will consist
of 50 1s and 50 0s, and so the sum of each row of A will be
exactly 50. If we drew a histogram of this distribution, it would be a
single spike at the number 50.
On the other hand, each call to
np.random.choice([0, 1], 2) could either return
array([0, 0]), array([0, 1]),
array([1, 0]), or array([1, 1]). Each of these
are returned with equal probabilities. In effect,
np.random.choice([0, 1], 2) flips a fair coin twice, so
[np.random.choice([0, 1], 2) for _ in range(50)] flips a
fair coin 100 times. When we take the sum of each row of B,
we will get the number of heads in 100 coin flips; the histogram drawn
is consistent with this interpretation.
Consider the function tom_nook, defined below. Recall
that if x is an integer, x % 2 is
0 if x is even and 1 if
x is odd.
def tom_nook(crossing):
bells = 0
for nook in np.arange(crossing):
if nook % 2 == 0:
bells = bells + 1
else:
bells = bells - 2
return bellsWhat value does tom_nook(8) evaluate to?
-6
-4
-2
0
2
4
6
Answer: -4.
np.arange(crossing) will evaluate to
[0,1,2,3,4,5,6,7]. Thus, the code contained within the loop
for nook in np.arange(crossing) will execute a total of 8
times and go into the if statement code 4 times and the
else statement code 4 times. After this execution, the
final value of bells comes out to -4.
Suppose we’re curious about how often a randomly formed group of
three students in EECS 398 will have three different majors. To explore
this, we created an array class_majors, which is an array
of every student’s major. For example, class_majors could
look something like
["DS", "CS", "Stats", "CS", "CE", "CS"].
Fill in the blanks below so that prob_all_unique is an
estimate of the probability that all three students selected are in
different majors.
Hint: The function np.unique, when called on an
array, returns an array with just one copy of each unique element in the
input. For example, if vals contains the values
1, 2, 2, 3, 3, 4, np.unique(vals) contains the
values 1, 2, 3, 4.
unique_majors = np.array([])
for i in np.arange(10000):
group = np.random.choice(class_majors, 3, __(a)__)
num_unique_majors = len(__(b)__)
unique_majors = np.append(unique_majors, num_unique_majors)
prob_all_unique = __(c)__What goes in blank (a)?
replace=True
replace=False
Answer: replace=False
Since we want to guarantee that the same student cannot be selected twice, we should sample without replacement.
What goes in blank (b)?
Answer: np.unique(group)
In each iteration of our for-loop, we’re interested in
finding the number of unique majors among the 3 students who were
selected. We can tell that this is what we’re meant to store in
unique_majors by looking at the options in the next
subpart, which involve checking the proportion of times that the values
in unique_majors is 3.
The majors of the 3 randomly selected students are stored in
group, and np.unique(group) is an array with
the unique values in group. Then,
len(np.unique(group)) is the number of unique majors in the
group of 3 students selected.
What goes in blank (c)?
(unique_majors > 2).mean()
(unique_majors.sum() > 2).mean()
np.count_nonzero(unique_majors > 2).sum() / len(unique_majors > 2)
1 - np.count_nonzero(unique_majors != 3).mean()
unique_majors.mean() - 3 == 0
Answer: Option 1
Let’s break down the code we have so far:
unique_majors is initialized to
store the number of unique majors in each iteration of the
simulation.np.unique function is
employed to identify the number of unique majors among the selected
three. The result is then appended to the unique_majors
array.unique_majors array contains a value greater than 2.Let’s look at each option more carefully.
(unique_majors > 2).mean() will create a Boolean array
where each value in unique_majors is checked if it’s
greater than 2. In other words, it’ll return True for each
3 and False otherwise. Taking the mean of this Boolean
array will give the proportion of True values, which
corresponds to the probability that all 3 students selected are in
different majors.(unique_majors.sum() > 2)
will generate a single Boolean value (either True or
False) since you’re summing up all values in the
unique_majors array and then checking if the sum is greater
than 2. This is not what you want. .mean() on a single
Boolean value will raise an error because you can’t compute the mean of
a single Boolean.np.count_nonzero(unique_majors > 2).sum() / len(unique_majors > 2)
would work without the .sum().
unique_majors > 2 results in a Boolean array where each
value is True if the respective simulation yielded 3 unique
majors and False otherwise. np.count_nonzero()
counts the number of True values in the array, which
corresponds to the number of simulations where all 3 students had unique
majors. This returns a single integer value representing the count. The
.sum() method is meant for collections (like arrays or
lists) to sum their elements. Since np.count_nonzero
returns a single integer, calling .sum() on it will result
in an AttributeError because individual numbers do not have a sum
method. len(unique_majors > 2) calculates the length of
the Boolean array, which is equal to 10,000 (the total number of
simulations). Because of the attempt to call .sum() on an
integer value, the code will raise an error and won’t produce the
desired result.np.count_nonzero(unique_majors != 3) counts the number of
trials where not all 3 students had different majors. When you call
.mean() on an integer value, which is what
np.count_nonzero returns, it’s going to raise an
error.unique_majors.mean() - 3 == 0 is trying to check if the
mean of unique_majors is 3. This line of code will return
True or False, and this isn’t the right
approach for calculating the estimated probability.We have a pool of 50 colleges, and would like to randomly select 4 of those colleges to form a bracket for our Mario Kart Tournament. Selection is performed uniformly at random, so that each team has the same chance of being selected. Please leave your answers in unsimplified form: answers of the form (\frac{3}{4}) \cdot (\frac{2}{3}) or \left[1 - (\frac{1}{2})^4\right] are preferred.
Assume we populate our tournament by randomly selecting four teams with replacement. What is the probability there are no duplicates among the four teams selected for the tournament? Do not simplify your answer.
Answer: \frac{1}{1} \cdot \frac{49}{50} \cdot \frac{48}{50} \cdot \frac{47}{50}
We need to find the probability that there are no duplicates among the four teams selected for the tournament from our pool of 50 with replacement. Since we are selecting four times, we want each selected team to be unique.
The total probability that there are no duplicates among the four teams selected is the product of these probabilities: \frac{1}{1} \cdot \frac{49}{50} \cdot \frac{48}{50} \cdot \frac{47}{50}
Now, assume we populate our tournament by randomly selecting four teams from our pool of 50 without replacement. Additionally, assume 30 are from Division 1 and 20 teams are from Division 2. What is the probability that there is at least one Division 2 team among the four teams selected for the tournament? Do not simplify your answer.
Answer: 1 - \frac{30}{50} \cdot \frac{29}{49} \cdot \frac{28}{48} \cdot \frac{27}{47}
We are selecting four teams from our pool of 50 without replacement, and we want to calculate the probability that at least one Division 2 team is selected, which represented as P(A). We know that there are 30 Division 1 teams and 20 Division 2 teams.
It’s much simpler to calculate the complement probability, P(Ac) which is the probability that all four teams are from Division 1, and then subtract from 1. Otherwise, we would have to calculate and add the probabilities of choosing 1, 2, 3, or 4 Division 2 teams - much more time consuming.
The probability that all four teams are from Division 1 is: \frac{30}{50} \cdot \frac{29}{49} \cdot \frac{28}{48} \cdot \frac{27}{47}
To find the probability of at least one Division 2 team being selected, we use P(A) = 1 - P(Ac): 1 - \frac{30}{50} \cdot \frac{29}{49} \cdot \frac{28}{48} \cdot \frac{27}{47}
Billina Records, a new record company focused on creating new TikTok audios, has its offices on the 23rd floor of a skyscraper with 75 floors (numbered 1 through 75). The owners of the building promised that 10 different random floors will be selected to be renovated.
Below, fill in the blanks to complete a simulation that will estimate the probability that Billina Records’ floor will be renovated.
total = 0
repetitions = 10000
for i in np.arange(repetitions):
choices = np.random.choice(__(a)__, 10, __(b)__)
if __(c)__:
total = total + 1
prob_renovate = total / repetitionsWhat goes in blank (a)?
np.arange(1, 75)
np.arange(10, 75)
np.arange(0, 76)
np.arange(1, 76)
What goes in blank (b)?
replace=True
replace=False
What goes in blank (c)?
choices == 23
choices is 23
np.count_nonzero(choices == 23) > 0
np.count_nonzero(choices) == 23
choices.str.contains(23)
Answer: np.arange(1, 76),
replace=False,
np.count_nonzero(choices == 23) > 0
Here, the idea is to randomly choose 10 different floors repeatedly, and each time, check if floor 23 was selected.
Blank (a): The first argument to np.random.choice needs
to be an array/list containing the options we want to choose from,
i.e. an array/list containing the values 1, 2, 3, 4, …, 75, since those
are the numbers of the floors. np.arange(a, b) returns an
array of integers spaced out by 1 starting from a and
ending at b-1. As such, the correct call to
np.arange is np.arange(1, 76).
Blank (b): Since we want to select 10 different floors, we need to
specify replace=False (the default behavior is
replace=True).
Blank (c): The if condition needs to check if 23 was one
of the 10 numbers that were selected, i.e. if 23 is in
choices. It needs to evaluate to a single Boolean value,
i.e. True (if 23 was selected) or False (if 23
was not selected). Let’s go through each incorrect option to see why
it’s wrong:
choices == 23, does not evaluate to a single
Boolean value; rather, it evaluates to an array of length 10, containing
multiple Trues and Falses.choices is 23, does not evaluate to what we
want – it checks to see if the array choices is the same
Python object as the number 23, which it is not (and will never be,
since an array cannot be a single number).np.count_nonzero(choices) == 23, does
evaluate to a single Boolean, however it is not quite correct.
np.count_nonzero(choices) will always evaluate to 10, since
choices is made up of 10 integers randomly selected from 1,
2, 3, 4, …, 75, none of which are 0. As such,
np.count_nonzero(choices) == 23 is the same as
10 == 23, which is always False, regardless of whether or
not 23 is in choices.choices.str.contains(23), errors, since
choices is not a Series (and .str can only
follow a Series). If choices were a Series, this would
still error, since the argument to .str.contains must be a
string, not an int.By process of elimination, Option 3,
np.count_nonzero(choices == 23) > 0, must be the correct
answer. Let’s look at it piece-by-piece:
choices == 23 is a Boolean array
that contains True each time the selected floor was floor
23 and False otherwise. (Since we’re sampling without
replacement, floor 23 can only be selected at most once, and so
choices == 23 can only contain the value True
at most once.)np.count_nonzero(choices == 23) evaluates to the number
of Trues in choices == 23. If it is positive
(i.e. 1), it means that floor 23 was selected. If it is 0, it means
floor 23 was not selected.np.count_nonzero(choices == 23) > 0 evaluates
to True if (and only if) floor 23 was selected.Suppose x and y are both ints
that have been previously defined, with x < y. Now,
define:
peach = np.arange(x, y, 2)Say that the spread of peach is the difference
between the largest and smallest values in peach. The
spread should be a non-negative integer.
Using array methods, write an expression that
evaluates to the spread of peach.
Answer: peach.max() - peach.min()
Without using any methods or functions, write an
expression that evaluates to the spread of peach.
Hint: Use [ ].
Answer:
peach[len(peach) - 1] - peach[0] or
peach[-1] - peach[0]
Choose the correct way to fill in the blank in this sentence:
The spread of peach is ______ the
value of y - x.
always less than
sometimes less than and sometimes equal to
always greater than
sometimes greater than and sometimes equal to
always equal to
Answer: always less than