from lec_utils import *

Discussion Slides: Cross-Validation and Regularization

Agenda 📆

• The bias-variance tradeoff.
• Cross-validation.
• Regularization.

The bias-variance tradeoff

• In the real world, we're concerned with our model's ability to generalize on different datasets drawn from the same population.

• In lecture, we trained three different polynomial regression models – degree 1, 3, and 25 – each on two different datasets, Sample 1 and Sample 2.
  The points in blue come from Sample 1.

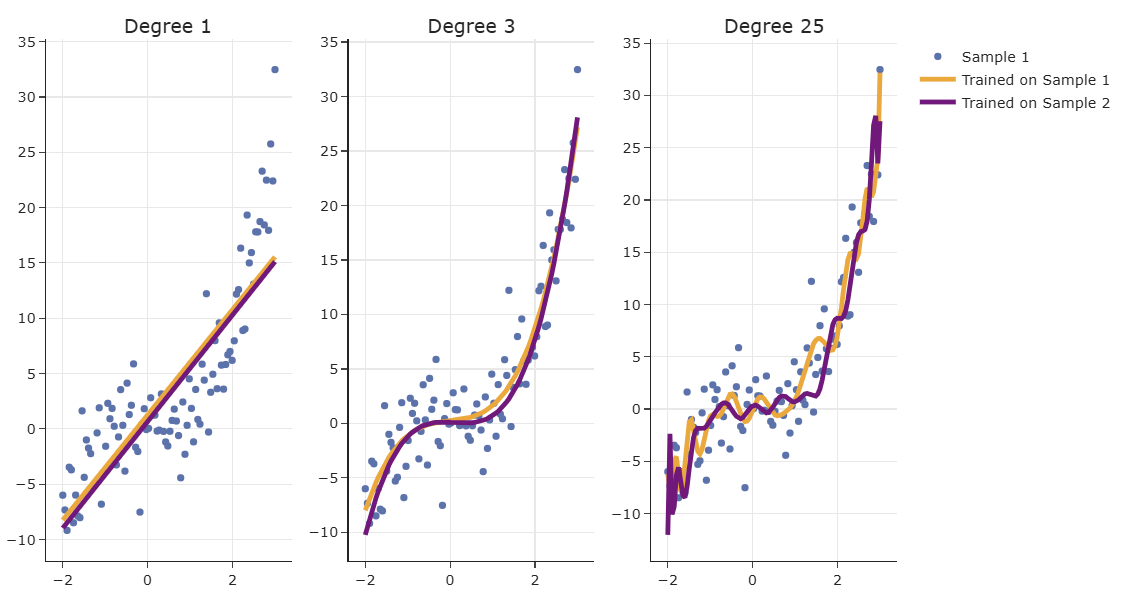
• The degree 1 polynomials have the highest bias – on average, they are consistently wrong – while the degree 25 polynomial has the lowest bias – on average, they are consistently good.

$$\text{low complexity} \rightarrow \text{underfits the training data} \rightarrow \text{high bias and low variance}$$

• The degree 25 polynomials have the highest variance – from training set to training set, they vary more than the degree 1 and 3 polynomials.

$$\text{high complexity} \rightarrow \text{overfits the training data} \rightarrow \text{low bias and high variance}$$

Cross-validation

• Cross-validation, as we talked about in lecture, is one way we can split our data into training and validation sets. We can create $k$ validation sets, where $k$ is some positive integer (5 in the example below).

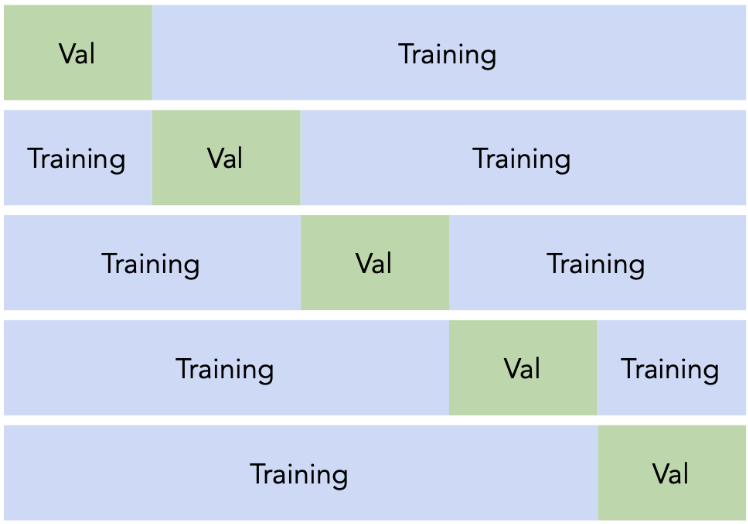
• Suppose we're choosing between 10 different hyperparameter values for our model and decide to use 5-fold cross-validation to determine which hyperparameter performs best.

• First, we divide the entire dataset into 5 equally-sized "slices".

• For each of the 10 hyperparameters, we perform 5 training rounds, for a total of 5 x 10 = 50 trainings.
  In each training, we'll use 4 folds to train the model and the remaining 1 fold to validate (test) it. This gives us 5 test error measurements per hyperparameter choice.

• Finally, we calculate the average validation error for each of our 10 hyperparameters, and choose the one with the lowest error.

• Aside: Some of the worksheet questions use the term "accuracy". Although we haven't covered it yet, accuracy is one of the ways to evaluate a classification model, where higher accuracy is better.

Regularization

• In general, the larger the optimal parameters $w_0^*, w_1^*, ..., w_d^*$ are, the more overfit our model is.
  We can prevent large parameter values by minimizing mean squared error with regularization.

$$R_\text{ridge}(\vec{w}) = \frac{1}{n} \lVert \vec{y} - X \vec{w} \rVert^2 \mathbf{+} \underbrace{\lambda \sum_{j = 1}^d w_j^2}_{\text{regularization penalty!}}$$

• Linear regression with $L_2$ regularization is called ridge regression.
  Linear regression with $L_1$ regularization is called LASSO.

• Intuition: Instead of just minimizing mean squared error, we balance minimizing mean squared error and a penalty on the size of the fit coefficients, $w_1^*$, $w_2^*$, ..., $w_d^*$.
  We don't regularize the intercept term!

• $\lambda$ is a hyperparameter, which we choose through cross-validation.
  • Higher $\lambda$ → stronger penalty, coefficients shrink more → higher bias, lower variance (underfitting).
  • Lower $\lambda$ → weaker penalty, coefficients can grow → lower bias, higher variance (overfitting).